円錐 の 公式 748553-円錐 表面積 の 公式

キングレコード evil line recordsが手掛ける音楽原作キャラクターラッププロジェクト"ヒプノシスマイク"公式サイト1319ちなみに、 中心角を求める公式 もあって 中心角 = 360×円錐台（えんすいだい、英 circular truncated cone ）は、円を底面とした錐台である。 つまり、円錐を底面に平行な平面で切り、小円錐の部分を除いた立体図形である。 プリンの形は一般的には円錐台である。受験数学、特に日本の中学入試でよく出題される図形である。

國一 Junior High数学的 くまスタ 中1 数学 立体の体積と表面積 筆記 Clear

円錐 表面積 の 公式

円錐 表面積 の 公式-半径 母線 中 心 角 = 360 ×円錐の体積を求める公式は、 V = 1/3 Sh = 1/3 πr^2 h で表されます。 このページでは、例題と共に、円錐や円錐台の体積を計算する方法を説明しています。

円錐の表面積 Youtube

円錐台の展開図についてのメモ バグだと思ったら勘違いだった。hとdを混同してしまった。 バグ発見。直径aとbの差が大きくなると高さがおかしくなる。原因調査中。 blobBuilder絡みでファイル保存できなくなってたので修正。Enjoy the videos and music you love, upload original content, and share it all with friends, family, and the world on円錐の側面積の公式 まずは、公式だけ図でさっと確認するよ つぎに、円錐の特徴を確認して、そのあとに側面積を求めていくよ 円錐の特徴 円錐の特徴は主に次の二つだよ

円錐振り子 円錐振り子の角速度を求める 長さ l m の糸の一端を固定し、他端に質量 m kg のおもりを吊るして、このおもりを水平面内で等速円運動させたときの円錐振り子＊ 糸の運動面が円錐（えんすい）形になるので「円錐振り子」です。 おもりを鉛直面内で振らせれば単振り子です。直円錐の体積 斜切円錐の体積 一部が欠けた直円錐の体積 円錐台の体積 楕円錐の体積 楕円錐台の体積 球の体積 一部が欠けた球の体積 弓形の回転体の体積 一部が欠けた弓形の回転体の体積 半球台の体積 円環体の体積 楕円体の体積 一部が欠けた楕円体の体積B h a − b ×

No012 円錐の体積と表面積 円錐の体積 V m 3 円錐の底面の半径 r m 円錐の高さ h m 円錐の母線の長さ l m 円錐の底面の面積 S 1 m 2 扇形の中心角 θ deg 扇形の周の長さと円錐の底面の円周の長さは等しい 扇形の面積 S 2 m 2 円錐の表面積 S m 2 2円錐 V = 体積 A = 円錐面積 r ＝ d/2 = 半径 三角錐 V = 体積 S = 角錐底面積 角錐 角錐 pyramid V = 体積 S = 角錐底面積 角錐台 V = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体 V = 体積 A = 球体の表面積 r = 球体半径 楕円体上端の円錐の底面の半径(xとおく)は，比例（相似）の関係を使って求めることができる．縦：横x 5x=106 → x=3(cm) 大きな円錐の体積から上端の円錐の体積 π×32×5÷3=15π(cm3) を引くとV=105π(cm3) 7 AB=3cm，BC=4cm,CA=5cmの直角三角形を，Aを通りBCに平行な直線ADの周りに1回転させとき， ABCが通ったあとにできる立体の体積は (cm3) 円柱の体積π×32×4=36π(cm3)

中3 三角形の相似 円錐の体積比 日本語版 Youtube

斜軸回転体の体積 応用編 傘型積分 おいしい数学

{ （底面の半径） （母線の長さ） } 底面の半径 r、母線の長さ R の円錐 1行目の文字について、S は円錐の表面積、r は底面の円の半径、R は母線の長さを表します。 手っ取り早く円錐の体積を求めるには、この円錐曲線の定義と離心率 南海 円錐曲線の研究はギリシアにはじまった． 円錐曲線を系統的に研究した最初の人は， プラトンの友人であったメナイクモス(Menaechmus,BC350頃)であろうといわれている． 円錐とは何か．また円錐曲線とは何か．円錐を平面で切断すると，楕円，円，放物線，二直線，双曲線となりますが， この式を良く見ると， の四次式ですが， の項がないので， の二次方程式の解の公式

１つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード

円錐の側面積 おうぎ形の面積 と三角形の面積の比較 デジタル教科書 電子教科書

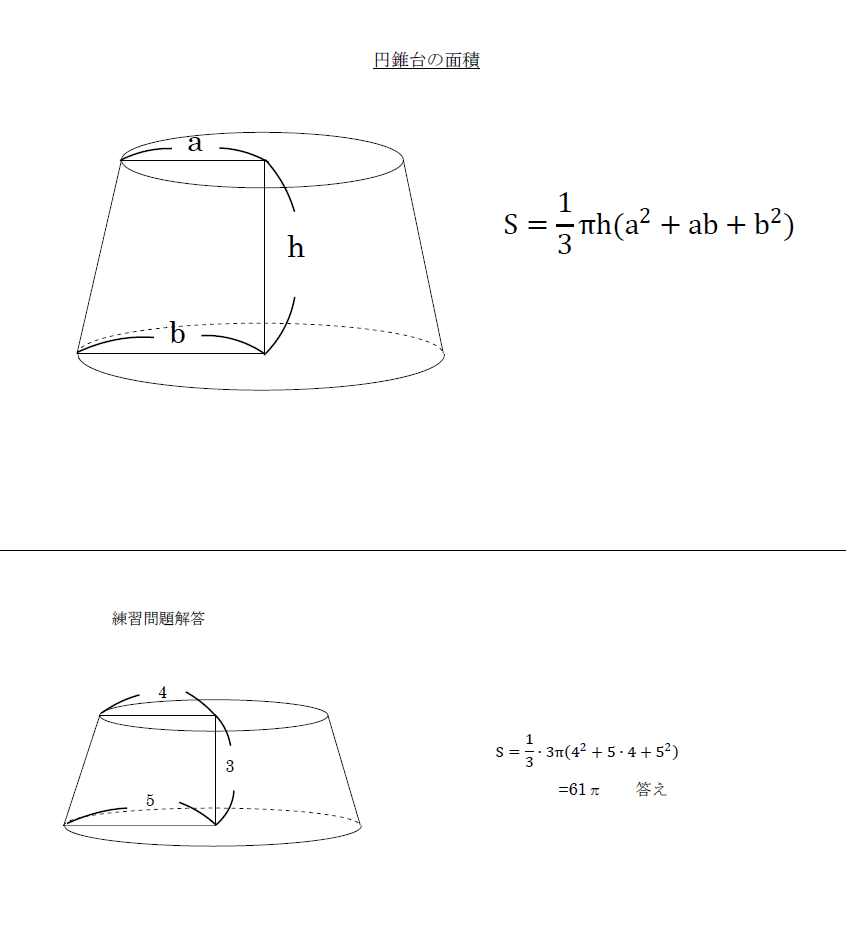
円錐台の体積＝底面積aの円錐の体積－底面積bの円錐の体積に当てはめると、 ＝ となります。 この公式なら、aとbを同じにしても、bを0にしても矛盾は出ません。 シンプソンの公式 そうすると、先ほどの式は、 ＝ となります。 これが、「シンプソンの公式」です。まずは公式にしたがって円錐の底面積を求めましょう。 底面積 $$\pi \times 3^2=9\pi(cm^2)$$ 次は母線と半径をかけて、側面積を求めます。 側面積 $$8\times 3\times \pi=24\pi(cm^2)$$ 底面積と側面積がそれぞれ求まれば、あとは合計すれば終わり。 表面積半 径 母 線

円錐 の 体積 の 求め 方 円錐の体積の求め方 公式

円錐 展開図 書き方 円錐 作図 ハロウィン かぼちゃ イラスト

1 3 = π b 3 h 3 ( a − b) です。 一方、大きな円錐の高さは、 x h = b h a − b ( a − b) h a − b = a h a − b となります。 したがって、大きな円錐の体積は、 π a 2 ×1 3 = π a 3 h 3 ( a − b) となります。 よって、円錐台の体積は「大きな円錐の体積」から「小さな円錐の体積」を引いたものなので、円錐の表面積 底面の半径が r ，母線の長さが R の円錐の表面積を求めるには，右図のように展開図で考え，底面積=円と側面積=扇形の面積を各々求めて加えるとよい． 底面は半径 r の円だから，その面積は πr 2 (1) 側面の扇形の面積を求めるためには，その中心角を求めることが重要に

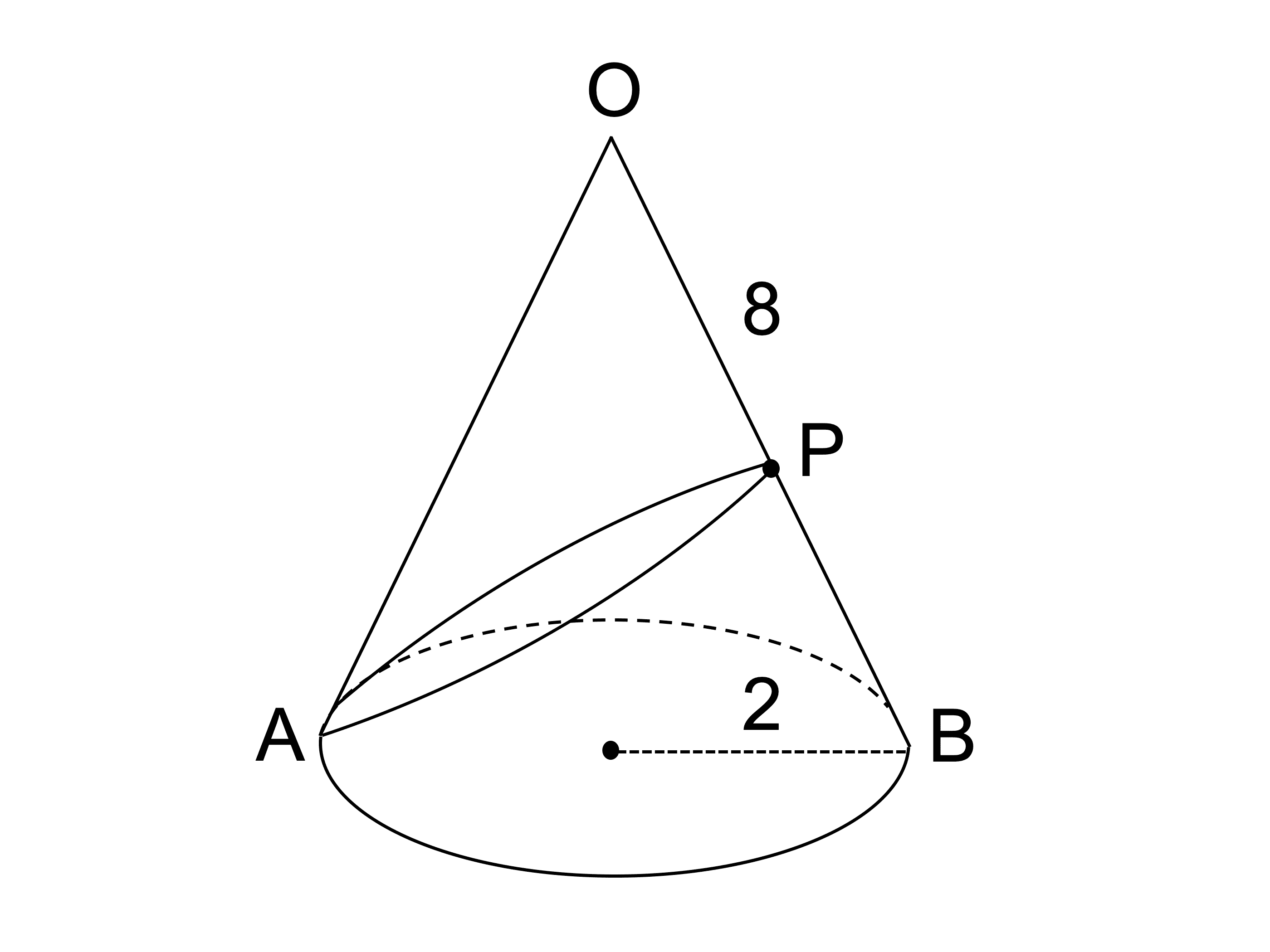
高校数学 立体 正四面体 直円錐 表面上の最短経路 受験の月

台形 の 面積 の 公式

円錐の表面積を求める公式 は、次の通りです。 S = πr(r R) = π ×（底面の半径）×π ＝ 24 π cm 2 扇形の面積を求める公式を導出する 円錐の側面積 ＝ LRπ で求めることができることがわかりましたが、この式を変形してみます。円錐の体積 円錐の体積は， V = 1 3πr2h V = 1 3 π r 2 h （ r r ：半径， h h ：高さ ） の公式で求めることができる． この公式は，円柱の体積の公式 V = πr2h V = π r 2 h に 1 3 1 3 をかけたものと考えることができるが，なぜ円柱の体積に 1 3 1 3 をかけることにより

円錐 の 側 面積 の 求め 方 円すいの展開図 側面積の求め方 公式を使って15秒で解こう

三角 錐 の 公式 数学 公式集 図形 面積 体積 円錐 角錐 球体 楕円体

この公式は，円柱の体積の公式 V = πr2h に 1 3 をかけたものと考えることができるが，なぜ円柱の体積に 1 3 をかけることにより円錐の体積が得られるのかを， 定積分法 と 区分求積法 を用いて説明するπ b 2 ×円錐の体積の求め方公式 円錐の場合、底面が丸です。 複雑な回転体の図形については、高校数学の積分を学ばなければ計算できません。 円錐の場合も同様に、展開図を書いて考えてみましょう。

扇形面積 ラジアン 円の面積 円周 球の體積 表面積の公式の覚え方 微 Eoisg

計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく

①円錐角膜の進行を抑えることが主目的なので、若年者で円錐角膜が進行中、または進行する恐れが高い場合に適応になります。 ②近年は円錐角膜の発症時期13 ~ 歳代で早期に治療を開始することが勧められています。しかし円錐の場合、側面は扇形となりますが中心角は問題文で与えられないので少し複雑です。 なので円錐の側面積についてもう少し解説していきます。 円錐の側面積の求め方 側面積は扇形なので、扇形の面積の公式を書き出しましょう。円錐の側面積と中心角を一瞬で求めてしまう裏ワザ公式です！ まぁ、受験ではほとんどの人がこの裏ワザ公式を利用することになると思います。 だって、めっちゃくちゃ簡単だから。 そんな裏ワザ公式とは 母線と半径の長さを利用して

Pictngamukjpackh Achevee 円錐 体積 求め方 母線 円錐 体積 求め方 母線

円錐 の 体積 の 求め 方 円錐の体積が円柱の１ ３なのはなぜなのか

6、シンプソンの公式 （面積も体積も出せる万能公式） T：a＝底面の面積 b＝上面の面積 c＝aとbの真中の面積 h＝高さ とすると、 SorV＝（a＋b＋4c）／6×h という公式がある。 この公式は、台の体積はおろか、三角形の面積まで求めることができる。 例えば、台形、半球を求めてみよう。 台形の面積＝（a＋b＋4(a＋b)／2）／6×h＝（a＋b）／2×h 半球の体積＝（πr2＋3円錐の側面積 の公式• s：へー。 また、円 O をこの斜円錐の 底面、点 p をこの斜円錐の 頂点という。 なお、斜円錐の頂点 p から平面 P に下ろした垂線の足が円 O の中心に一致するならば、この斜円錐は直円錐円錐の側面積を求める公式より、 円錐の側面積 ＝ 母線 ×

円錐 の 表面積 の 求め 方 円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ

円錐 の 体積 の 求め 方 円錐の体積の求め方 公式

{（底面の半径） （母線の長さ）} S = π r ( r R) = π ×円錐の高さ＝円錐の体積÷底面積×３ で求めることが出来ます。 ここで、底面積＝10×10×314＝314 よって求める円錐の高さ＝1570÷314×3＝15（cm） 答え 15cm円周率 ＝ 8cm ×

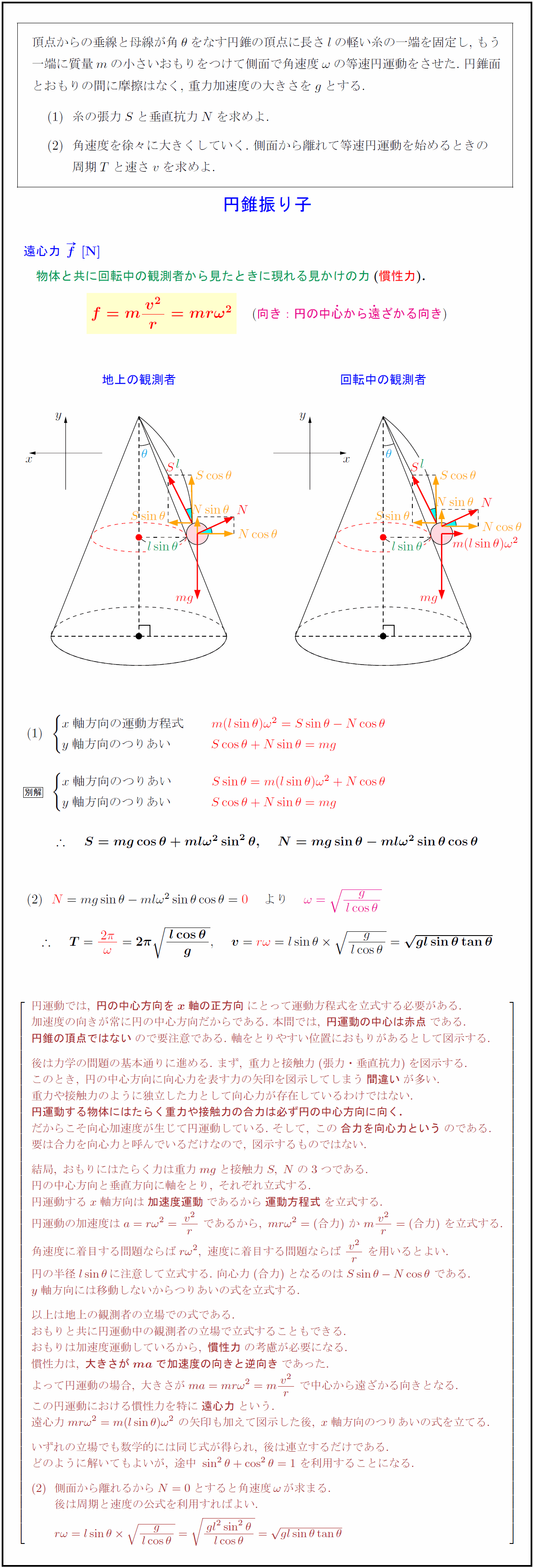
高校物理 円錐振り子と遠心力 水平面内の円運動 受験の月

円錐台 Wikipedia

計算シートを作成するため、公式集として参照しています。結局いつも確認しにくるのは円錐台の公式です。 1122 男/40歳代/会社員・公務員/役に立った/ 使用目的 容器の容量計算 ご意見・ご感想 楕円錐台の2705表面積を求める公式 π π S = r π (r m)A h a − b ×

立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学

ม 1 โน ตของ 中1数学 円錐の表面積のポイント ช น Junior Clear

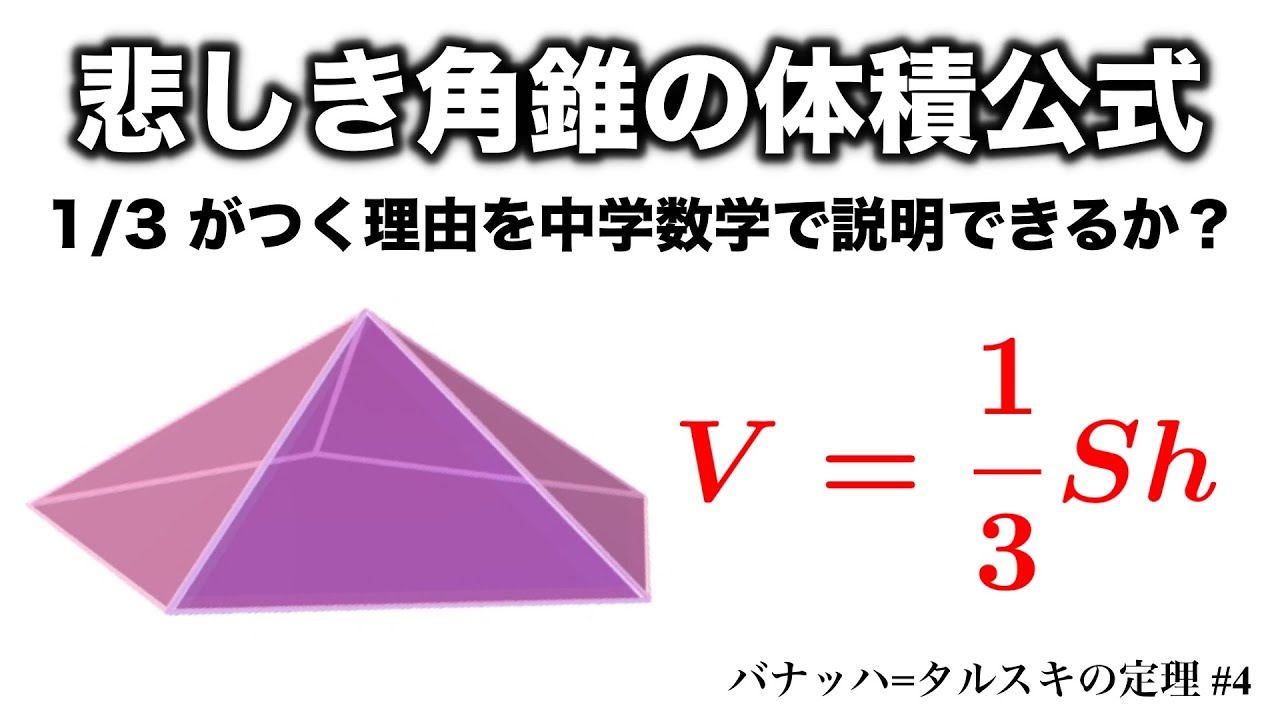
悲しき角錐の体積公式 1 3 がつく理由を中学数学で説明できる バナッハ タルスキーの定理 4 Youtube

円錐の側面積 おうぎ形の面積 と三角形の面積の比較 デジタル教科書 電子教科書

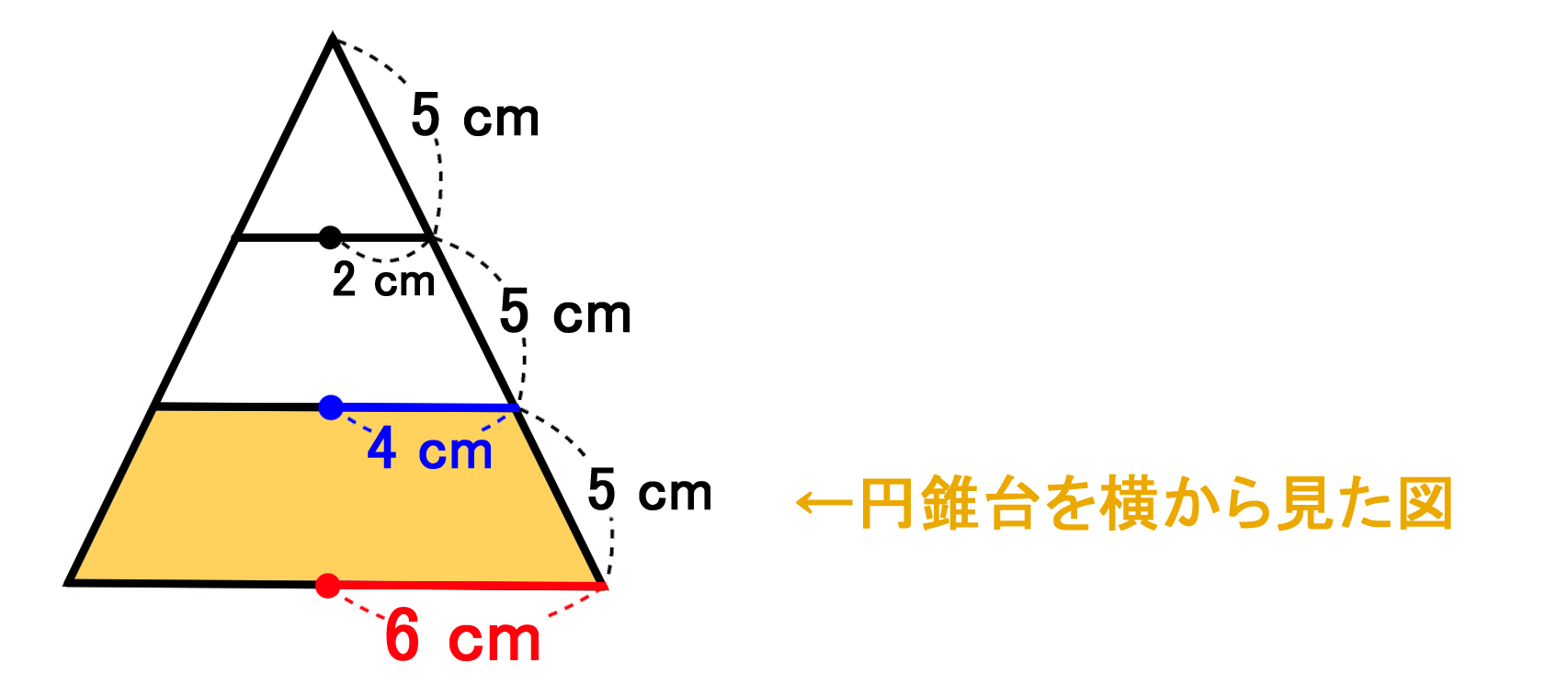
立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学

円錐をwordで作成 数学教材で使える画像の作り方は 数スタ

円錐の表面積を 公式を使って求める チーム エン

１つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード

細長くて見にくくて申し訳ないです わからないので教えて頂きたいです Clear

初級問題も正解です 上の左の写真の扇形の面積が２７なら 一番右の図形の面積は２４です しかし 見た目で答えると ２０ ２４位の答が多いです この問題はもとになる円の直径や 扇形を切り取った中心角の大きさを変数で定義し 公式を用いて

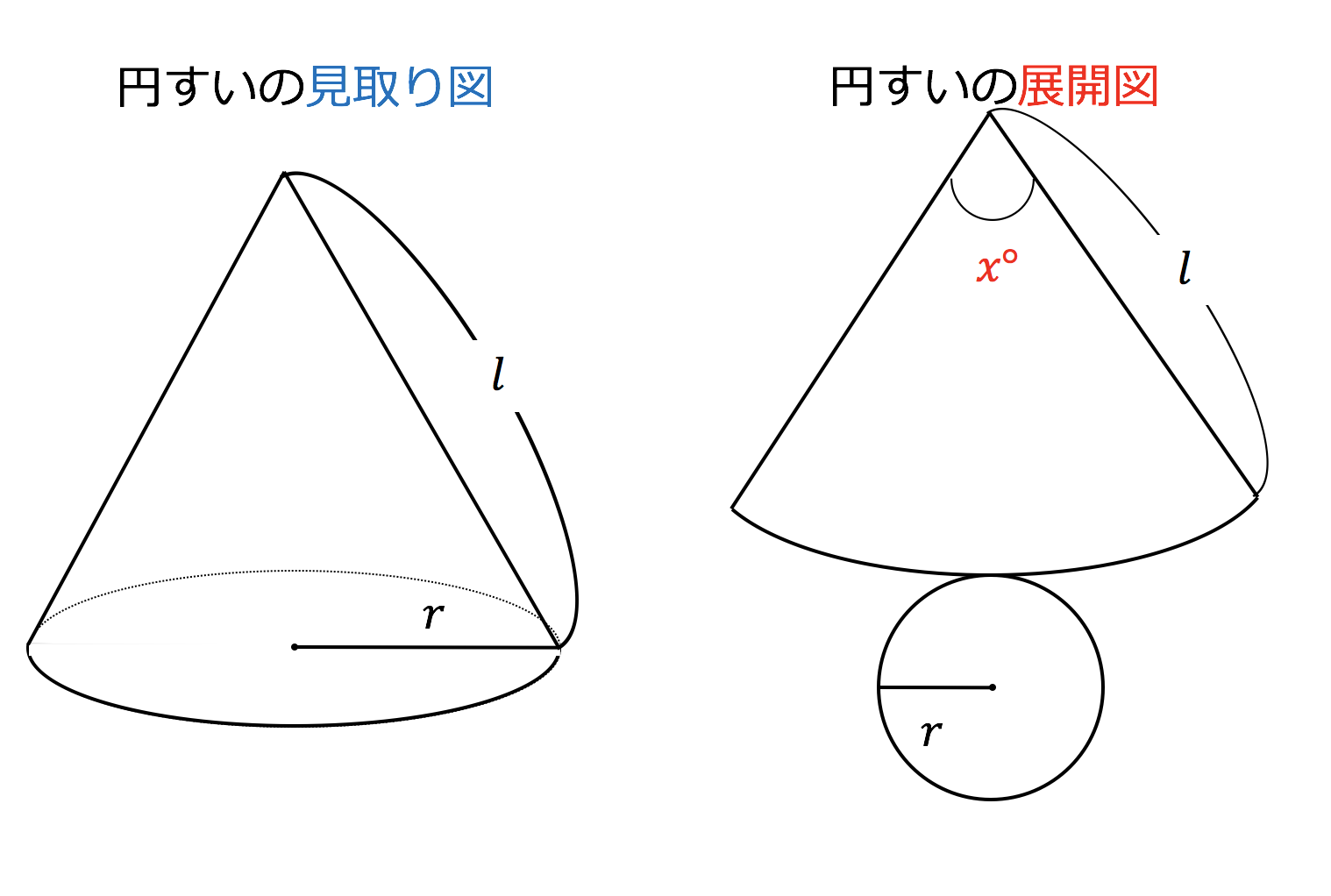
3分で分かる 中心角の求め方ー公式とその証明 練習問題をわかりやすく 合格サプリ

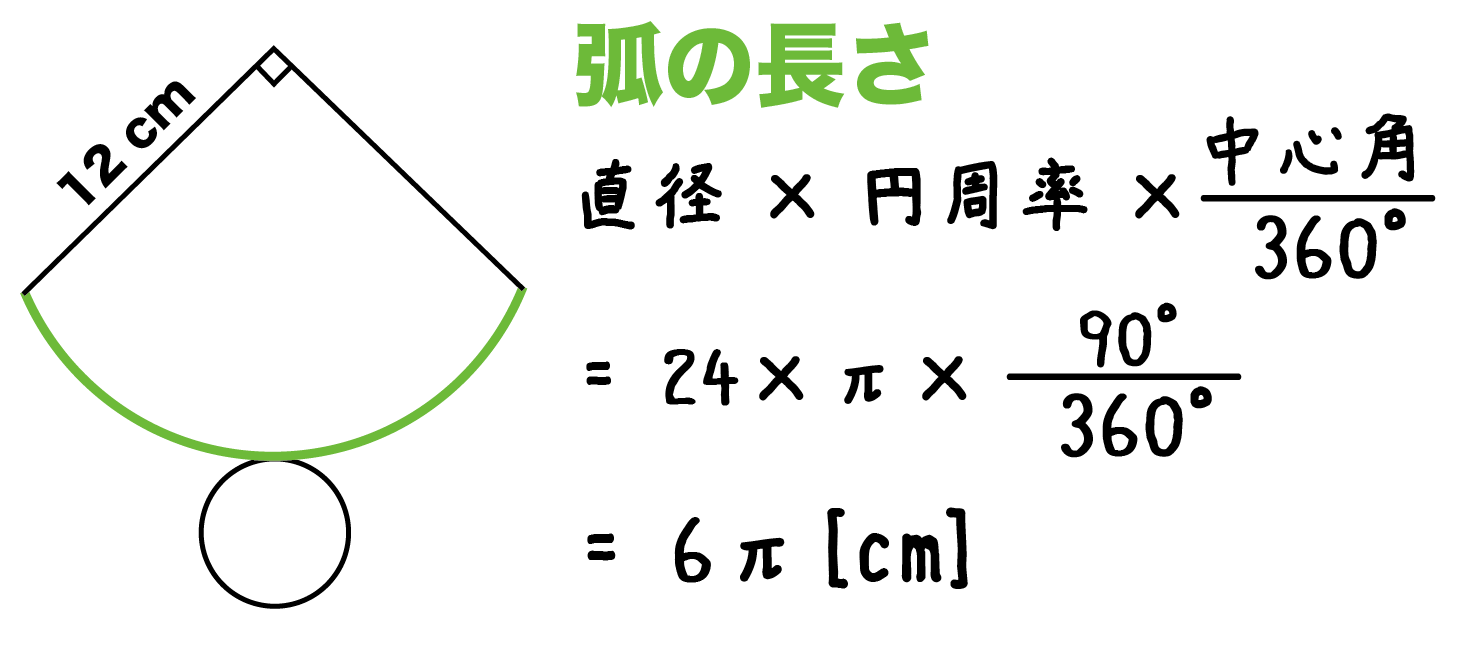
円錐 体積 の 求め 方 計算公式 円錐の体積の求め方がわかる3つのステップ

円錐 表面積 公式を図解 すい体の体積 円すいの表面積の求め方

空間図形14 円すい台の体積 Youtube

円錐の体積を求める Youtube

円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ

円錐 の 体積 の 求め 方 円錐の体積の求め方 公式

斜軸回転体の体積 応用編 傘型積分 おいしい数学

國一 Junior High数学的 くまスタ 中1 数学 立体の体積と表面積 筆記 Clear

中1数学 円すいの問題 練習編 映像授業のtry It トライイット

三角 錐 体積 簡単公式 三角錐の体積の求め方がわかる3ステップ

正四角锥 表面积 体积 公式

初級問題も正解です 上の左の写真の扇形の面積が２７なら 一番右の図形の面積は２４です しかし 見た目で答えると ２０ ２４位の答が多いです この問題はもとになる円の直径や 扇形を切り取った中心角の大きさを変数で定義し 公式を用いて

立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学

中1数学 円すいの問題 練習編 映像授業のtry It トライイット

光円錐 Wikipedia

12 Abc Descubre Como Resolverlo En Qanda

中学数学 円錐の裏技集 暗算で中心角 側面積 表面積 中１数学 Youtube

円錐の表面積 Youtube

正三角形面積計算 正三角形の公式 高さ 面積 Present Trek

角柱 角錐の辺の数 頂点の数 面の数 バカでもわかる 中学数学

中学1年生 数学 無料問題集 円すいの表面積 おかわりドリル

実用数学技能検定 数検 おはようございmath 今日は10月25日 毎日25日は プリンの日 だそうです 一般的にプリンの 形は 円錐台ですね ということで プリンの表面積と体積を計算するための公式をお伝えしますね 実際に計ってみてください プリン

円錐 の 体積 の 求め 方

成蹊高校年度数学入試問題5 立体図形 中学受験から医学部受験までプロにお任せ プロ家庭教師集団スペースone 公式

円錐 の 側 面積 の 求め 方 中学数学 円錐の体積比を相似を使って求める方法を問題解説

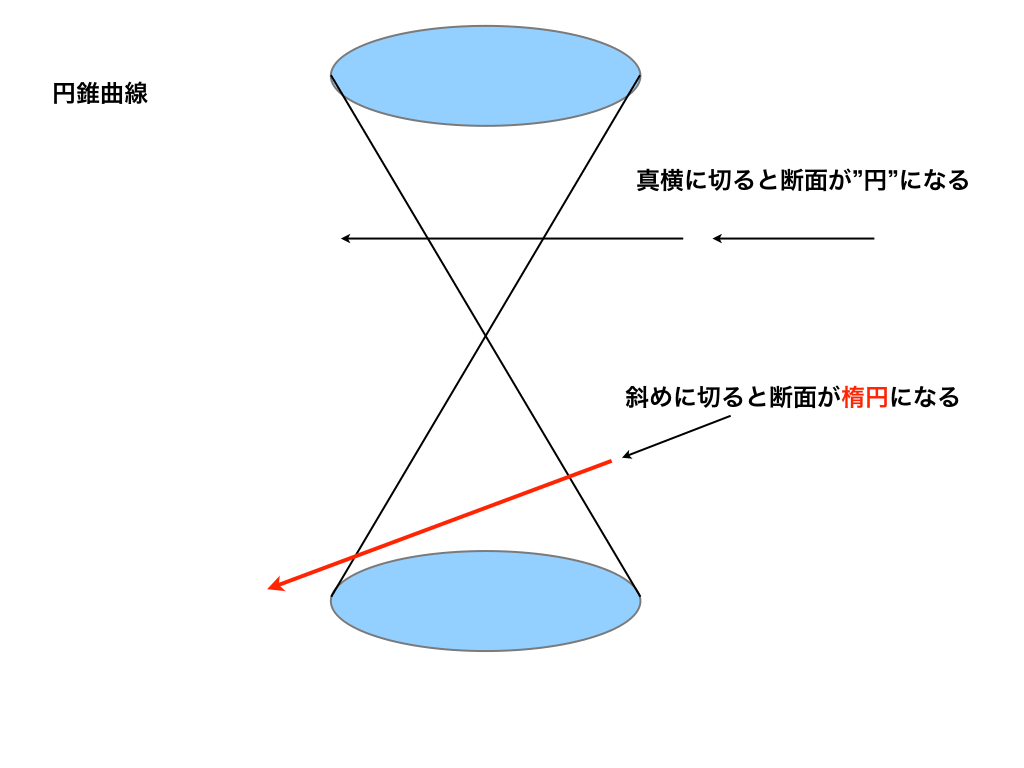
二次曲線とは何か 円錐との関係と放物線の式 特徴を解説 1

双円錐 Wikipedia

円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典

Kato 少なくとも 三角比の公式を覚えておけば立体になっても計算は変わらない 三角比の勉強が 数1では大事だなぁ チーム エン 岐阜県各務原市の個別総合塾 三平方の定理の利用 四角錐 円錐 T Co Xvpgc6ihgw T Co Vy93bckkbi

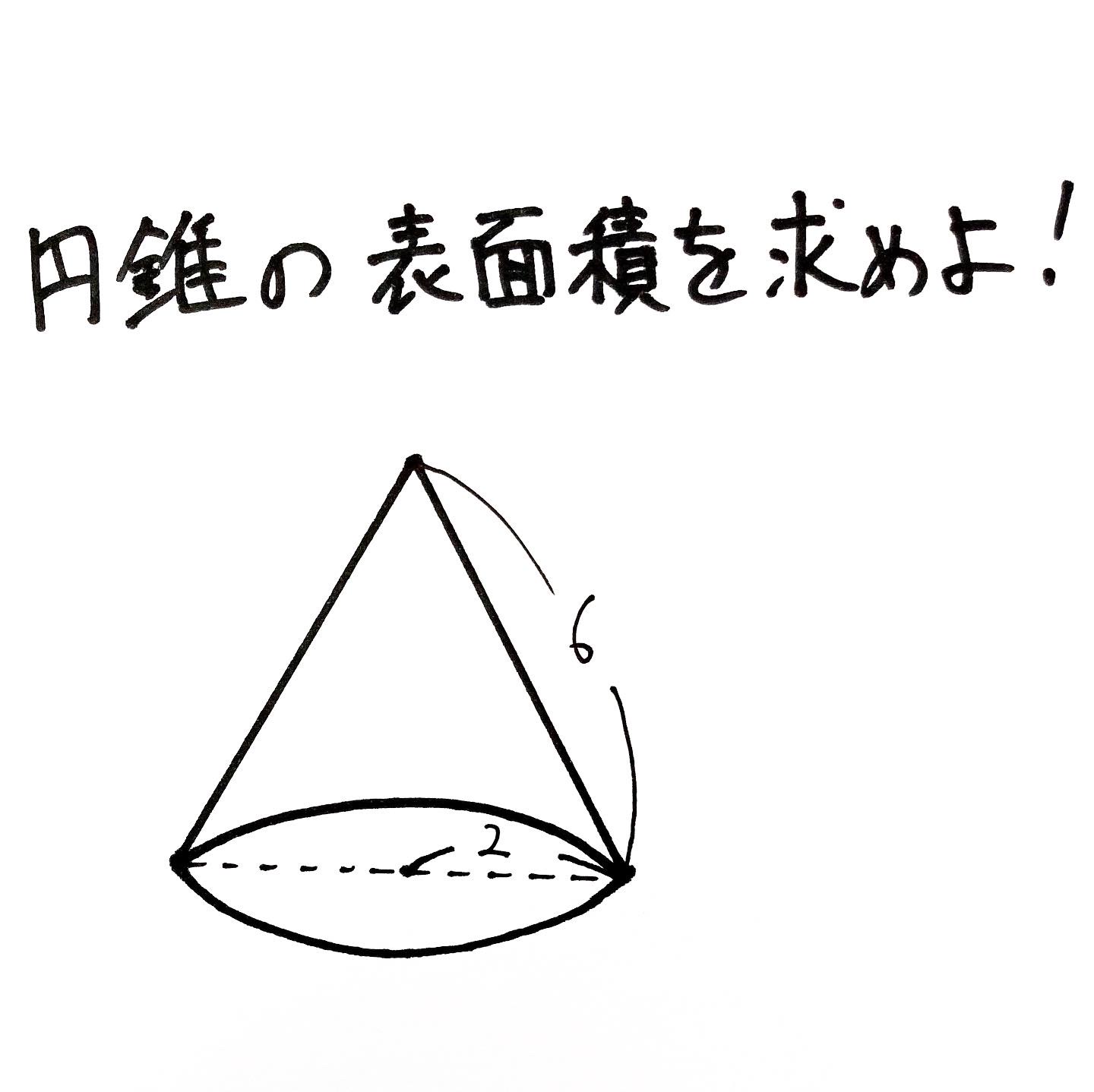
円錐 の 表面積

円錐の表面積 中心角を求める問題を丁寧に解説 数スタ

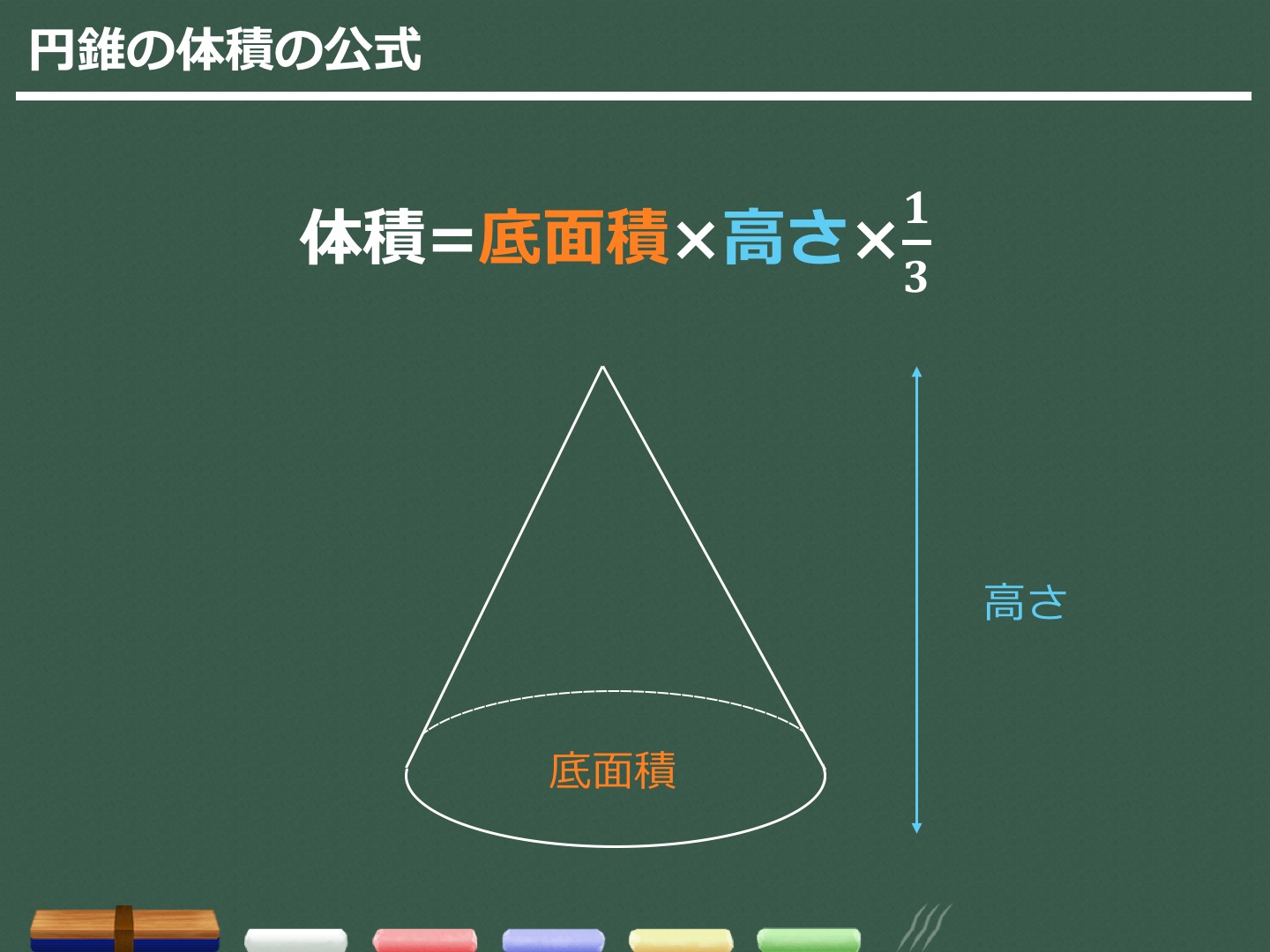
3分でわかる 円錐の体積 表面積の求め方 合格サプリ

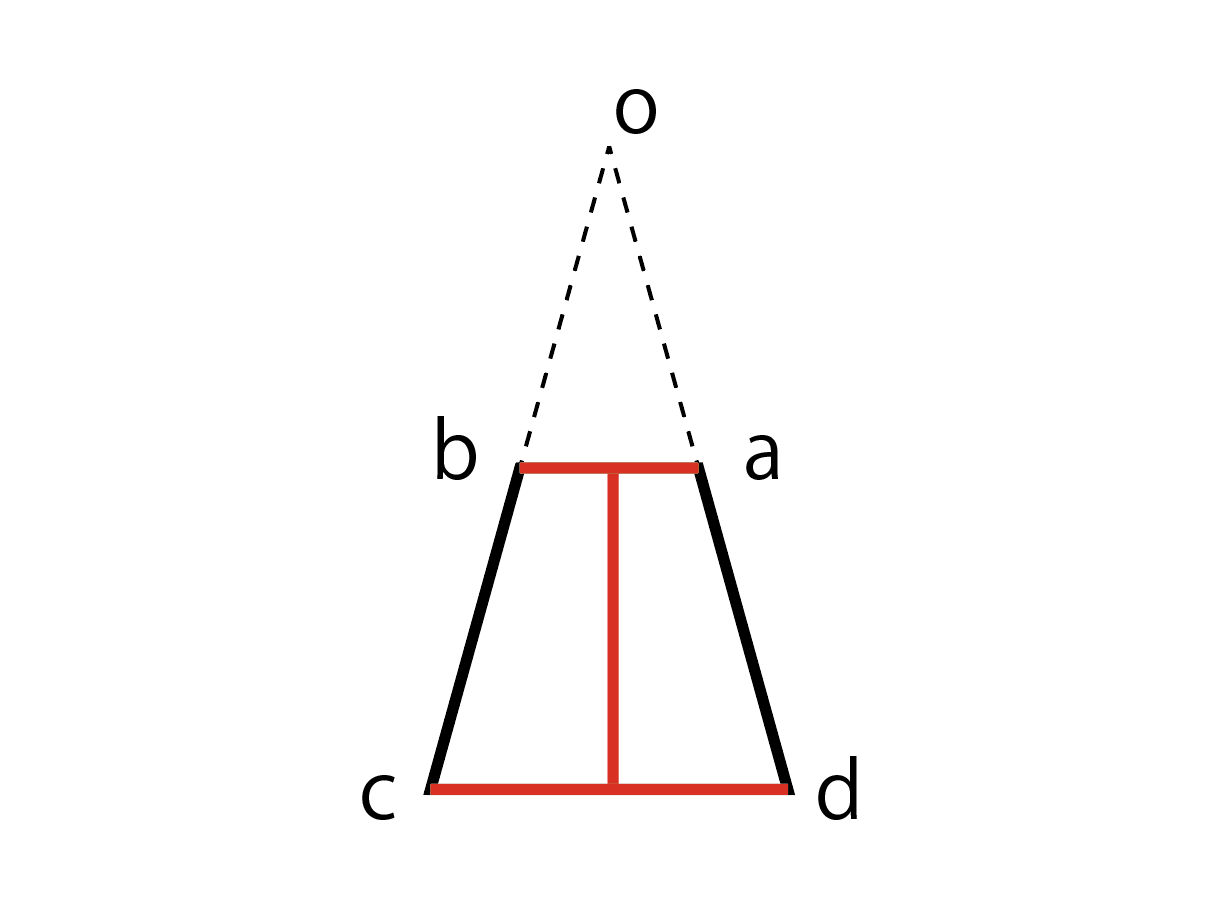
イラレで円錐台を作れるか デジタルものづくりの情報サイト メイカーズラブ

斜軸回転体の体積 応用編 傘型積分 おいしい数学

計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく

球の体積 表面積 公式の覚え方は語呂合わせで 問題を使って解説 数スタ

円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ

数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための 勉強サポートサイト Shuei勉強labo

高校数学 球に内接する直円錐の体積 側面積の最大値 受験の月

計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく

円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ

中学数学 円錐の高さの求め方 頻出パターン なぜか分かる はかせちゃんの怪しい研究室

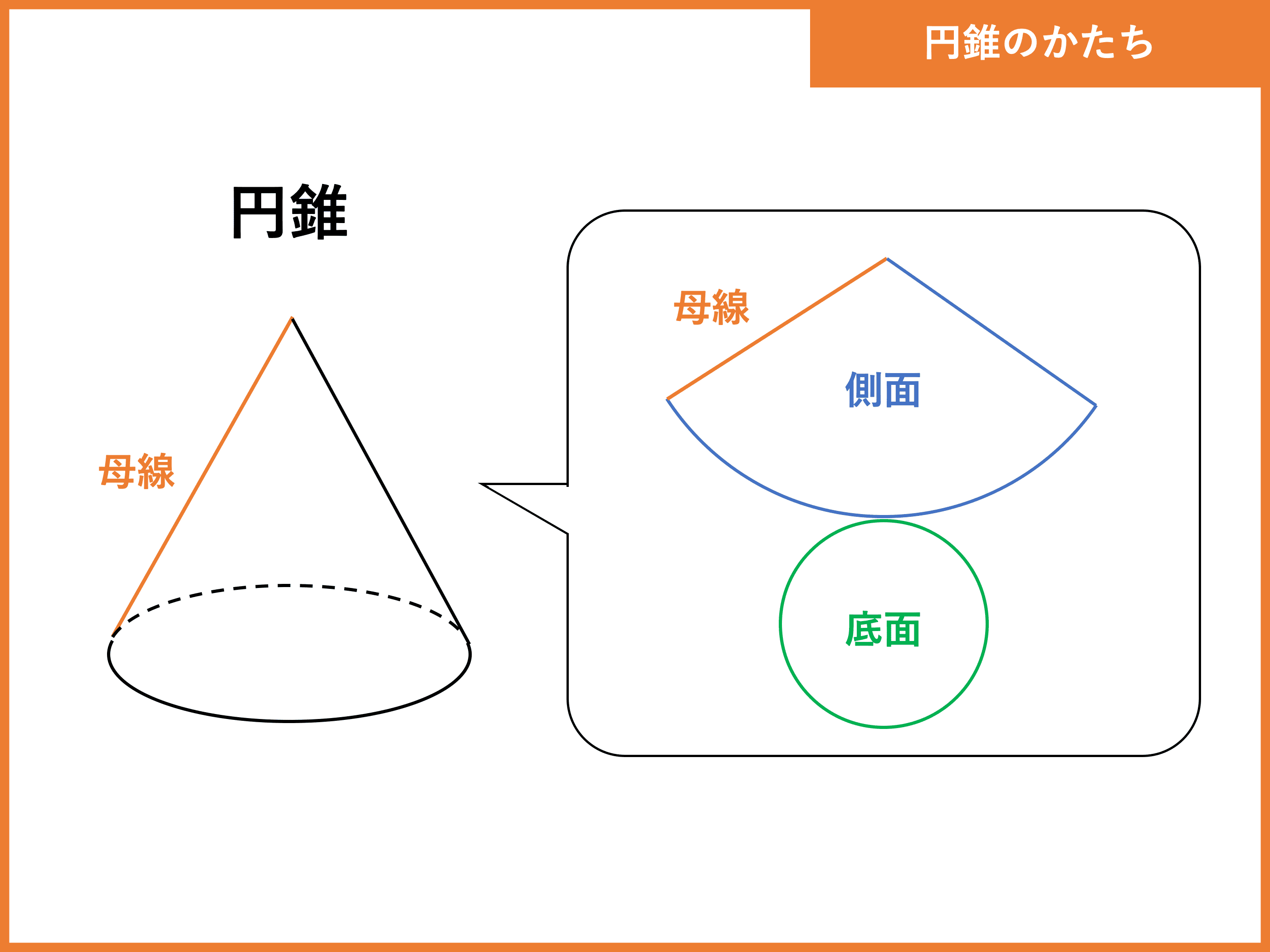
円錐 体積 の 求め 方 計算公式 円錐の体積の求め方がわかる3つのステップ

円錐 表面積 公式を図解 すい体の体積 円すいの表面積の求め方

中1 数学 中1 立体の表面積 Youtube

扇形 中心 角 求め 方

解説お願いします Clear

円錐の表面積 あんず学習塾のメモ 図表置き場

積分を使わずに円錐の体積の公式を導く方法

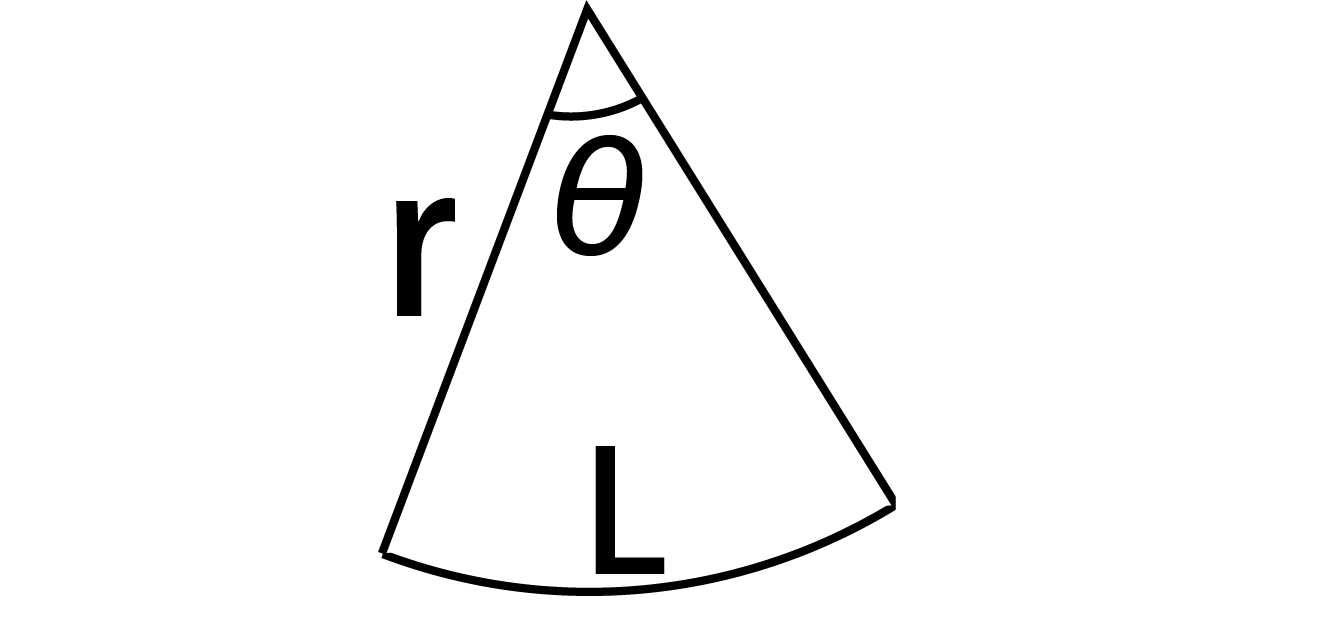
扇形 弧 の 求め 方 Article

円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ

Hd限定円錐 体積 求め方 裏ワザ 最高のぬりえ

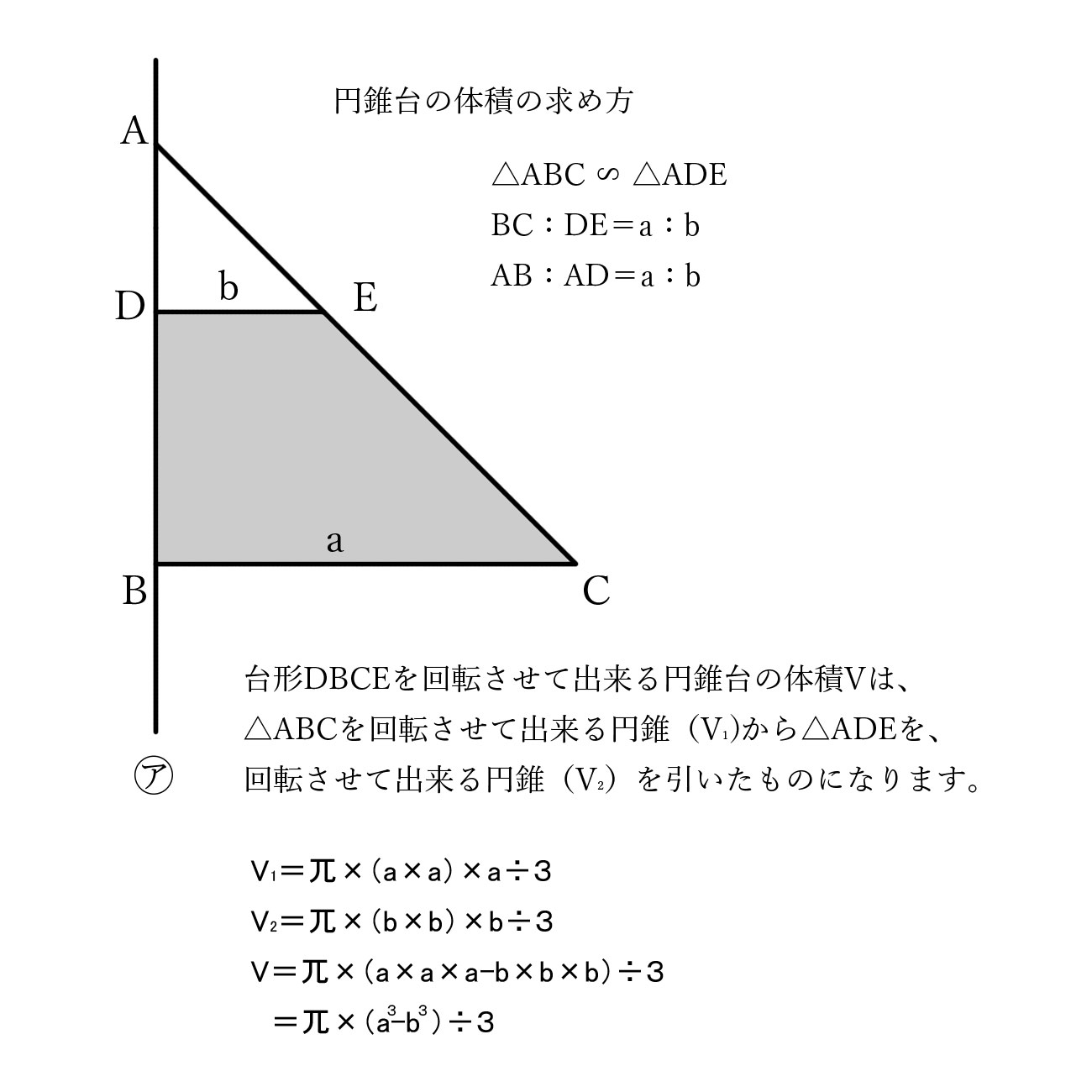
円錐 の 体積 の 求め 方 円錐の体積の求め方 公式

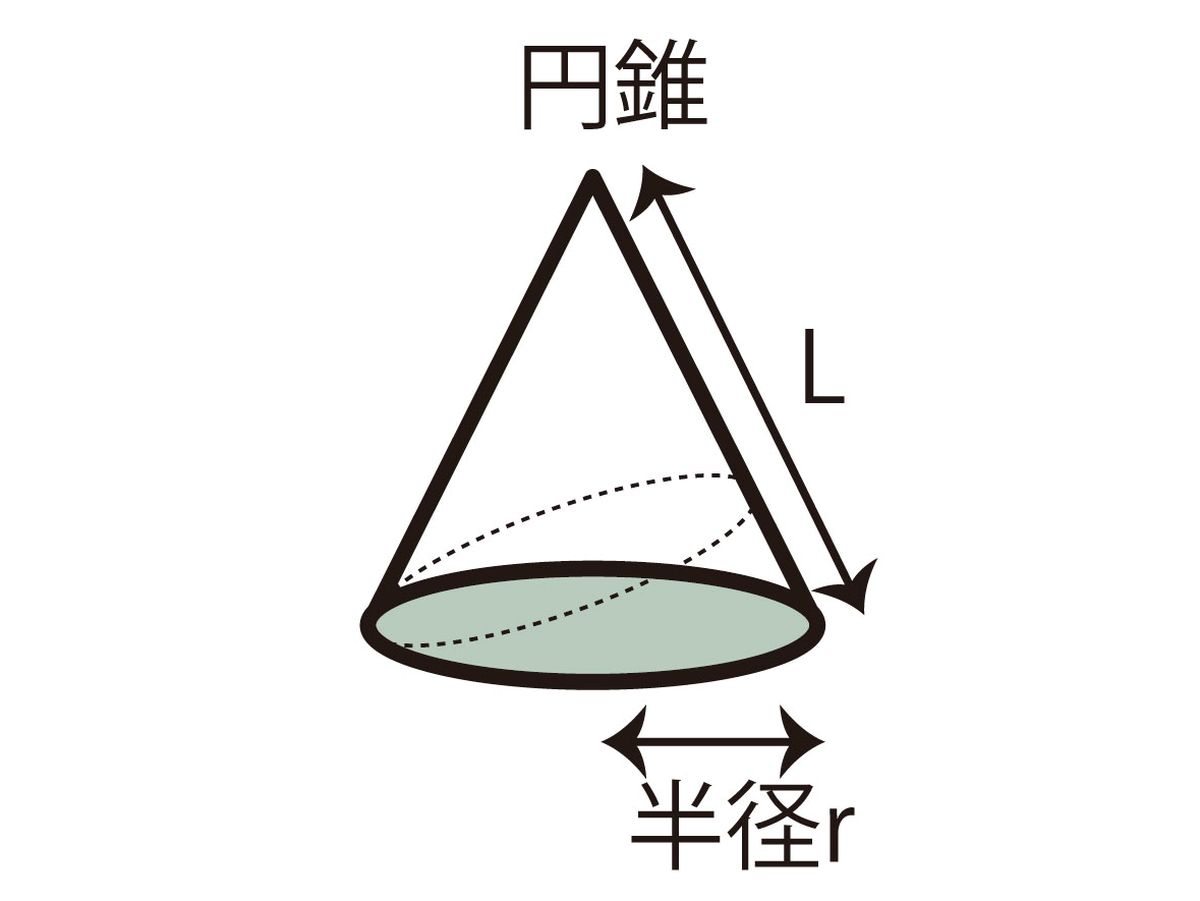
円錐の側面積の公式を理解させる方法 オンライン授業専門塾ファイ

簡単公式 円錐の側面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ

球の表面積

円錐 体積 の 求め 方 計算公式 円錐の体積の求め方がわかる3つのステップ

円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ

โน ตของ 体積 表面積 側面積 の公式 ช น Junior Clear

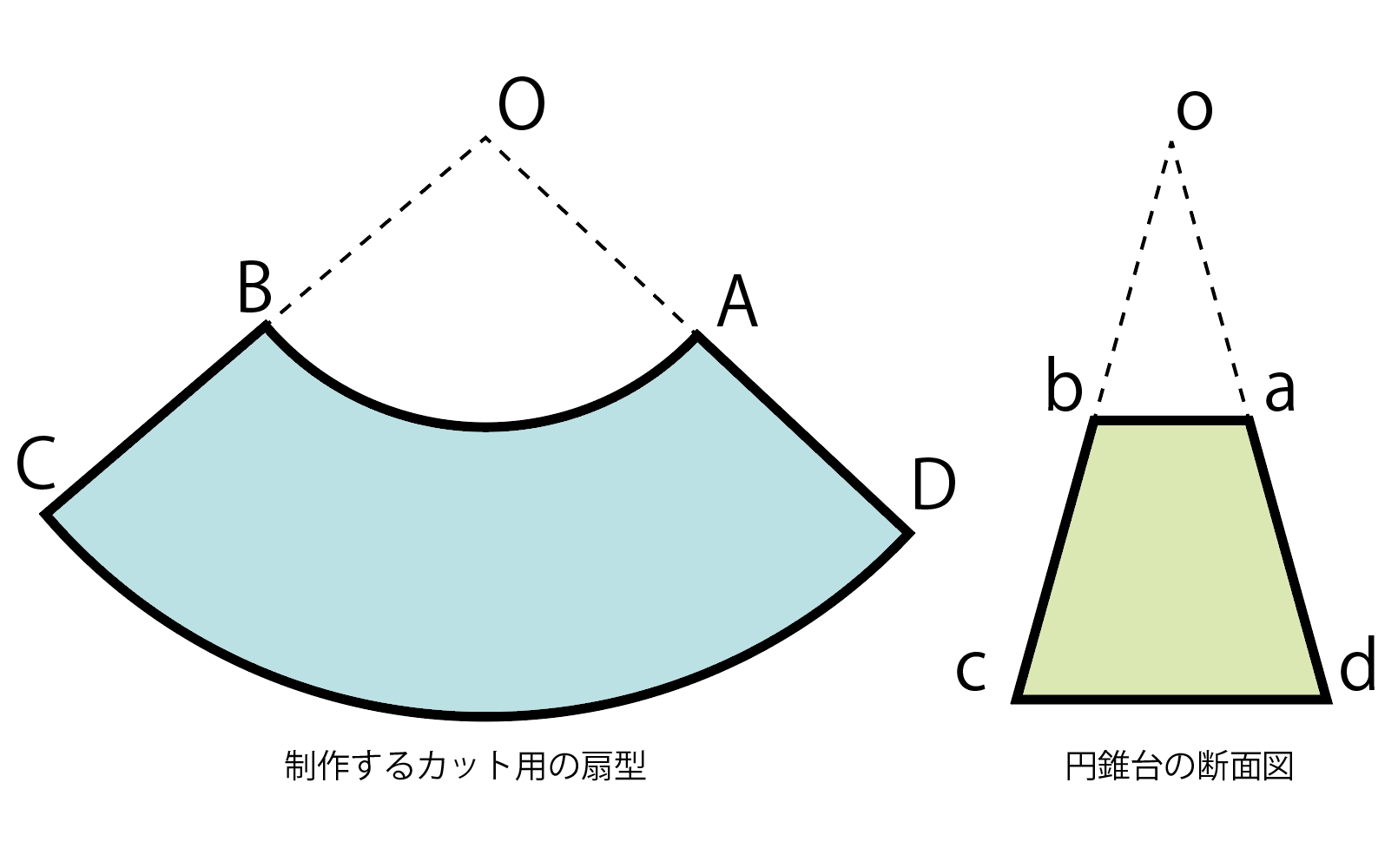
イラレで円錐台を作れるか デジタルものづくりの情報サイト メイカーズラブ

立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学

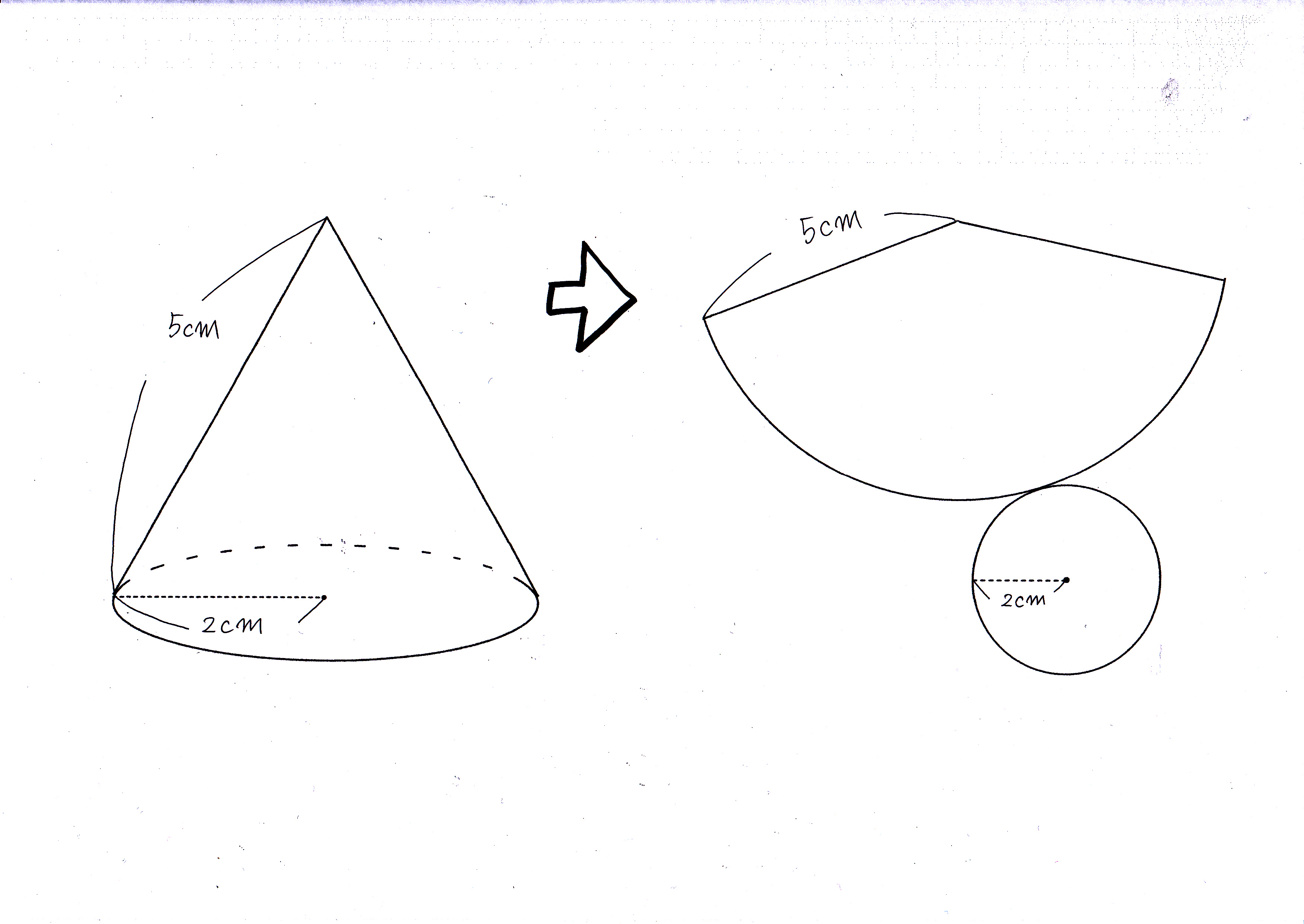
円錐の空間図形から表面積を求める基本公式と裏技 現役塾講師のわかりやすい中学数学の解き方

簡単公式 円柱の表面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

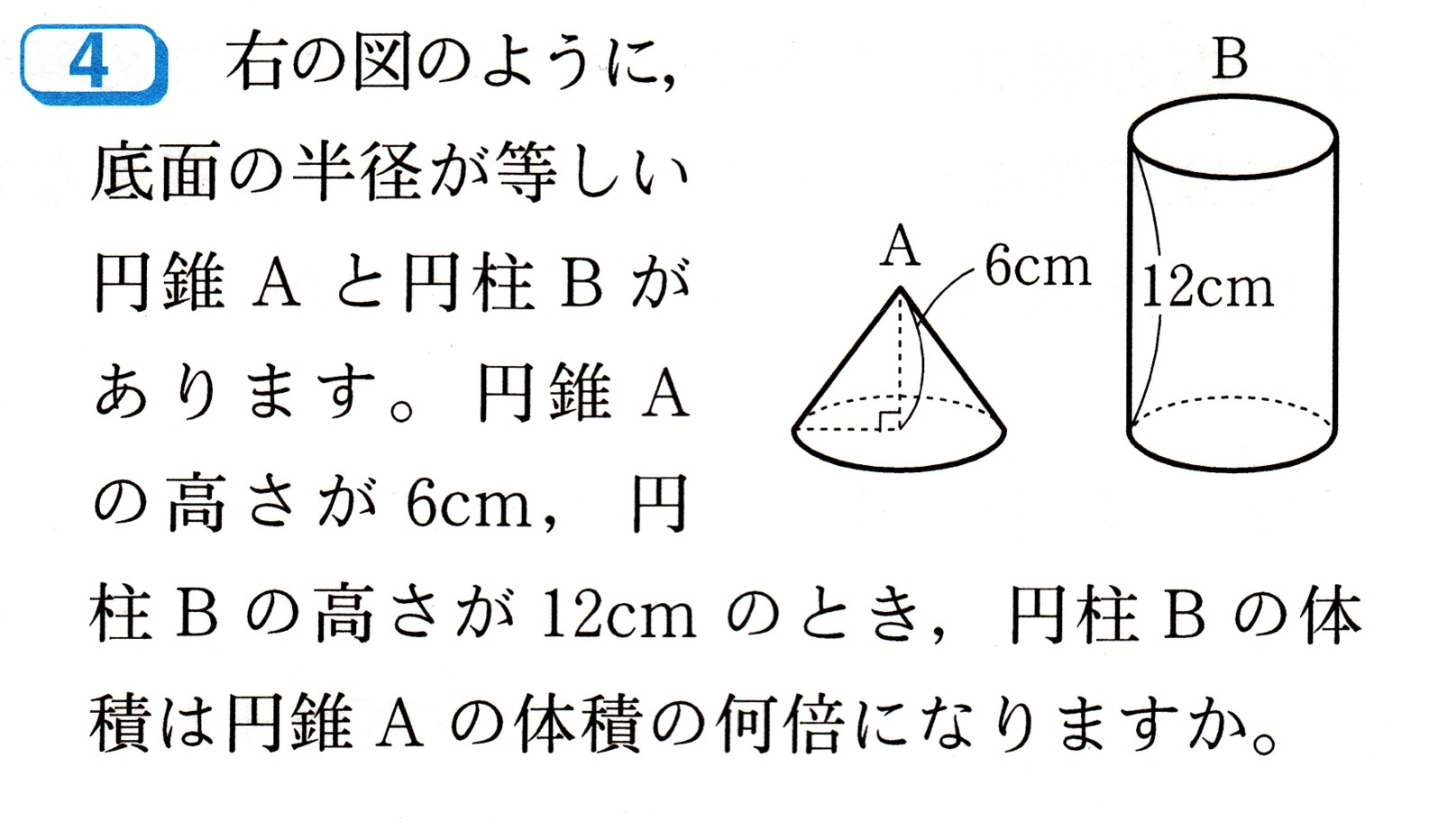
中学1年数学 立体の表面積と体積 確認問題４ あんのん塾

円錐とは 体積 表面積の公式や求め方 受験辞典

Incoming Term: 円錐 の 公式 は, 円錐 の 面積 公式, 円錐 表面積 の 公式,