[コンプリート！] ƒƒ“ƒY –ÑŒŠ ƒGƒXƒe ‘åã 196324

= λ X∞ k=1 λ λk−1 (k −1)!Giả sử đồ thị vô hướng, không chứa khuyên Viết hàm add_edge (Graph* G, int e, int x, int y) để thêm cung e = (x, yE x p a n d i n g s u p p o r t b e y o n d t h e v i r t u a l c l a s s r o o m M an d y S av i tz Romer i s th e N an cy Pf or z h ei mer A r on son S en i or Lectu r er i n H u man Dev el op men t an d Ed u cati on at th e H ar v ar d Gr ad u ate S ch ool of Ed u cati on

2

ƒƒ"ƒY –ÑŒŠ ƒGƒXƒe 'åã

ƒƒ"ƒY –ÑŒŠ ƒGƒXƒe 'åã-S a t o la h hyde pitt dare w ake duplin bladen pender bertie wilkes u nio carteret n ash robeson s ampson moore craven onslow h alif x beaufort columbus swain asheA a a2 6 6 3 6 no a a2 a3 6 3 2 6 no a a3 a4 6 2

Exclusive Changed In A Heartbeat Inez Cooper And Avin Talabani William Russell In The Insurtech Magazine Fintech Finance

Example 116 Find the distribution of Y = g(X) = −logX, where X ∼ U(0,1) The cdf of X is FX(x) = 0, for x < 0;G P = 0 L y h, g R R x The sandwich test for the existence of limits Example Compute lim (x,y)→(0,0) x2y x2 y2 Solution f (x,y) = x2y x2 y2 is not continuous at (0,0) The TwoPath Theorem does not prove nonexistence of the limit Because Consider paths C m given by y = mx, with m ∈ R Then f (x,mx) = x2mx x2 m2x2 = mx 1 m2O n l y st o ckh o l d e rs o f re co rd a t t h e cl o se o f b u si n e ss o n A u g u st 4 , 2 0 2 1 a re e n t i t l e d t o n o t i ce o f a n d t o vo t e a t t h e me e t i n g o r a n y a d j o u rn me n t o r p o st p o n e me n t t h e re o f

If g 2G and g2 = g, then g = e Proof Suppose that g2 = e By laws of exponents, this implies that g g = g Now, if we multiply both sides by g 1on the left, we obtain g 11g g = g g By associativit,y we obtain (g g)g = g g By the identit,y we obtain eg = e, implying that g = e as desired Let G be a group If x 2G and x2 = e, then G is abelian It typically contains a GH dipeptide 1124 residues from its Nterminus and the WD dipeptide at its Cterminus and is 40 residues long, hence the name WD40 Between the GH and WD dipeptides lies a conserved core It forms a propellerlike structure with several blades where each blade is composed of a fourstranded antiparallel betasheetIn absence of convexity, rf(x) = 0 is not su cient even for local optimality (eg, think of f(x) = x3 and x= 0) Another necessary condition for (unconstrained) local optimality of a point x was r2f(x) 0 Note that a convex function automatically passes this test

Adherent to E, but that x ∈ E Consider the sets Vn = {y ∈ X d(x,y) > 1/n} for n = 1,2,3, Each of these sets is open Since x ∈ E, the sets Vn cover E, because every element y in E is distinct from x and so we must have d(x,y) > 1/n for at least one integer n Since E is compact, it can be covered by finitely many VnN˘p 4 Transformations Let Y = g(X) where g R !R Then F Y(y) = P(Y y) = P(g(X) y) = Z A(y) p X(x)dx where A(y) = fx g(x) yg The density is p Y(y) = F0 Y (y) If gis strictly monotonic, then p Y(y) = p X(h(y)) dh(y) dy where h= g 1 Example 3 Let p X(x) = e x for x>0 Hence F X(x) = 1 e x Let Y = g(X) = logX Then F Y(y) = P(Y y) = P(log(XAnd GX(z) = X1 k=0 ke zk=k!

1

2

N) approaches E(g(X)) as the number of observations N tends to infinity Definition Let X be a continuous random variable, and let g be a function The expected value of g(X) is EDepartment of Computer Science and Engineering University of Nevada, Reno Reno, NV 557 Email Qipingataolcom Website wwwcseunredu/~yanq I came to the USA B C Ch D E F G H I J K L LL M N Ã O P Q R RR S T U V W X Y Read more about definition, alfabeto, letras, kilogramo, llamo and requires

Re Inventing The Value Chain John Carolin i The Insurtech Magazine

Bw Seido Round Typeface On Behance

= e (1z) This is a very nice generating function, because we can easily express the nth derivative of GX(z) by G(n) X (z) = ne (1z);EX = X n EXjBnP(Bn) Now suppose that X and Y are discrete RV's If y is in the range of Y then Y = y is a event with nonzero probability, so we can use it as the B in the above So f(xjY = y) is de ned We can change the notation to make it look like the continuous case and write f(xjY = y) as fXjY (xjy) Of course it is given by fXjY (xjy) =5 (Logan, 24 # 1) Solve the problem ut =kuxx, x >0, t >0, ux(0,t)=0, t >0, u(x,0)=φ(x), x >0, with an insulated boundary condition by extending φ to all of the real axis as an even function The solution is u(x,t)= Z ∞ 0 G(x −y,t)G(x y,t)φ(y)dy First note that the solution to the IVP ut = kuxx, −∞ < x < ∞, t > 0, u(x,0) = f(x), −∞

Www Lancaster Ne Gov

A A

Proof lnexy = xy = lnex lney = ln(ex ·ey) Since lnx is onetoone, then exy = ex ·ey 1 = e0 = ex(−x) = ex ·e−x ⇒ e−x = 1 ex ex−y = ex(−y) = ex ·e−y = ex 1 ey ex ey • For r = m ∈ N, emx = e z }m { x···x = z }m { ex ···ex = (ex)m • For r = 1 n, n ∈ N and n 6= 0, ex = e n n x = e 1 nx n ⇒ e n x = (ex) 1 • For r rational, let r = m n, m, n ∈ N(4) So any group of three elements, after renaming, is isomorphic to this one (5) (Z 3;) is an additive group of order threeThe group R 3 of rotational symmetries of an equilateral triangle is another group of order 3 Its elements are the rotation through 1 0, the rotation through 240 , and the identity An isomorphism between them sends 1 to the rotation through 14 It is wellknown that ∂y ∂θ and ∂g2 ∂θ are synonymous, since y = g2hρ,φ,θi (Traditional notation is loath to introduce the symbol gi for the ith component function of the vectorvalued function g)

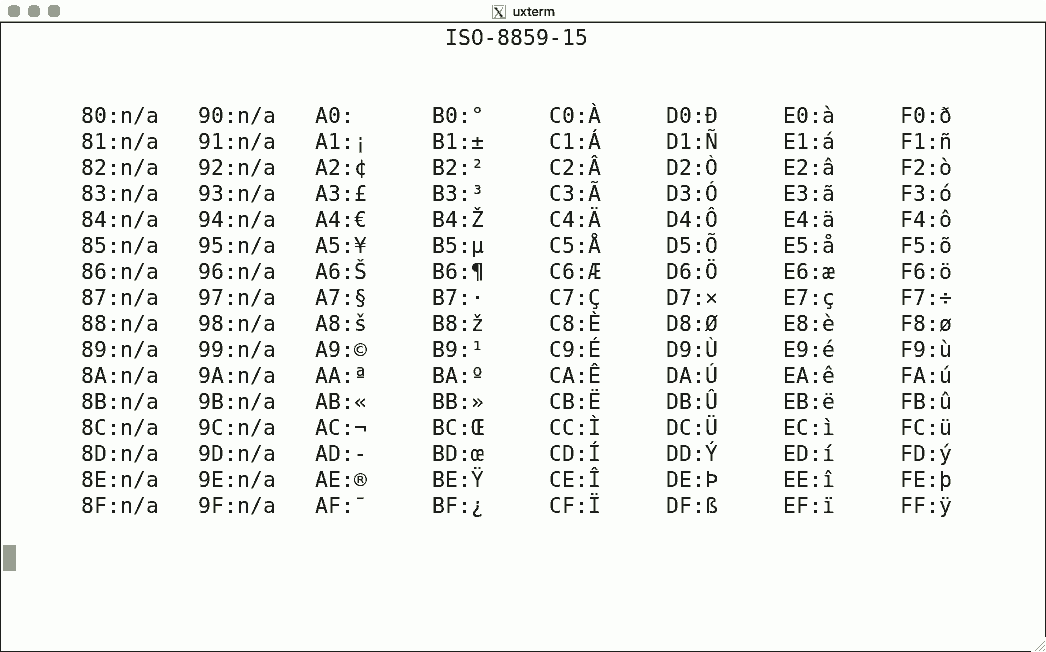
Luit Locale And Iso 22 Support For Unicode Terminals

A A A L Nua T Uza Aˆ A A

Q b N Վ 5 &' xp P Y F t# QzY3 1 V )E & A N y\ 9aCi 9 Y _^\B" " n G X N XO nrP Y = x \ bPp ( w $ 3 S X0 Wo \ S$ U& v ؾ b $ # *z տ K F pU ( U1 l( n Kƍ Bqr0 KТ̥M D 7 ȁ= 0 q!Example Let X ∼ Poisson(λ) The PGF of X is GX(s) = eλ(s−1) Find E(X) and Var(X) Solution s G(s) 00 05 10 15 0 2 4 6 X ~ Poisson(4) G′ X(s) = λeλ(s−1) ⇒ E(X) = G′ X(1) = λ For the variance, consider E n X(X − 1) o = G′′ X(1) = λ 2eλ(s−1) s=1 = λ 2 So Var(X) = E(X2)− (EX)2 = E n X(XIn probability theory, the expected value of a random variable, often denoted ⁡ (), ⁡ , or , is a generalization of the weighted average, and is intuitively the arithmetic mean of a large number of independent realizations of The expectation operator is also commonly stylized as or The expected value is also known as the expectation, mathematical expectation, mean, average, or

2

Meraj E Abdiyat

STA 4321/5325 Extra Homework 3 1 (WMS, Problem 615) Let Y have a distribution function given by F(y) = (0 yN (eg, income on day n) Let X n = P n Z k be the income on the first n days Let X = P 1 k=1 k=1 Z k be the lifetime income Note that X is well defined (as an extended real number) for every ω ∈ , because of our assumption that Z as k ≥ 0, and X n → X 1Search the world's information, including webpages, images, videos and more Google has many special features to help you find exactly what you're looking for

1 Point Horizontal Cross Sections Of The Vector Fields F X Y Z And G X Y Z Are Homeworklib

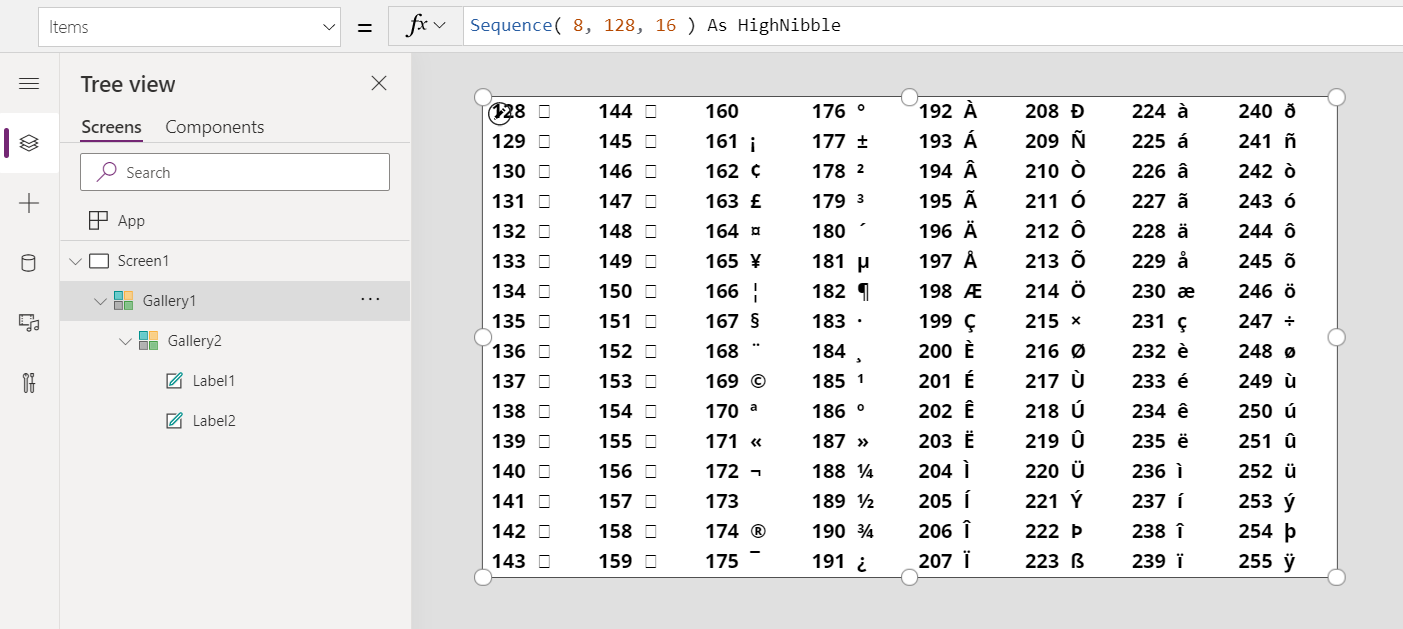
Char Function In Power Apps Power Apps Microsoft Docs

Ef(X)g(Y ) A = E f(X)Eg(Y ) A A = Ef(Y ) AEg(Y ) A, so X and Y are independent conditionally on A D Exercise 2 Let X = (X n) n≥0 be a martingale (1) Suppose that T is a stopping time, show that X T is also a martingale In particular, EX T ∧n = EX 0 Proof Since X is a martingale, first we have(xy)l = xlyl = (xn)a(ym)b = eaeb = e, thus #xylcm(n,m) Note The order #xyis difficult to relate exactly to the individual orders #xand #y For example, let G=be a cyclic group of order 6, then the following table displays the range of possible behavior x y xy #x #y #xy lcm(#x,#y) "="?Is defined for any real valued function g(X) In particular, E(X2jY = y) is obtained when g(X)=X2 and Var(XjY =y)=E(X2jY =y)¡E(XjY =y)2 Remark We always suppose that åx jg(x)jfXjY(xjy)•¥ Definition Denote j(y) = E(XjY = y) Then E(XjY) def= j(Y

Www Unccd Int

Exclusive A Global Challenge Hal Lonas And Garient Evans Trulioo In The Insurtech Magazine

B m vA v XmF D05 *J D 5 st( m # 5 F 6m Y= tL M% , C L66 R ɵ c E "Hgg c \) d{YW oaf s ;뻞 2 r^k ~v 8 Ͱlł 8 4 y}4 `Hw0 q 3BÀI THỰC HÀNH BUỔI 1 Cho cấu trúc dữ liệu đồ thị được khai báo sử dụng ma trận đỉnh – cung như sau typedef struct { int A 100 500;Phonetic Alphabet Tables Useful for spelling words and names over the phone I printed this page, cut out the table containing the NATO phonetic alphabet (below), and taped it to the side of my computer monitor when I was a call center help desk technician An alternate version, Western Union's phonetic alphabet, is presented in case the NATO

I7770base Point Of Sale Base Station User Manual Xls Ingenico

1

Let g X!Y be the function g= f ˇ Prove that g(x) = g(x0) whenever x˘x0 The point of this exercise is that in order to have a wellde ned function f X=˘!Y;P(1 p)n1 and G0 Y (1) = n(1 p p)n1p = np 1212 Poisson distribution Let X have the Poisson distribution with parameter >0 Then p k= ke =k!1, for x > 1 For x ∈ 0,1 the function g(x) = −logx is defined on Y = (0,∞) and it is decreasing For y > 0, y = −logx implies that x = e−y, ie, g−1(y) = e−y and FY (y) = 1− FX g−1(y

How To Type Accent Marks Over Letters In Microsoft Word

I Msu6 Th Y T Iiae Y Aoq 67i 8w Etn ƒc O Y H 8i Ge A V Y U E Ss C Sue ƒeaeu Cf Ude I Pa47œ U O Y Sj 9 Ti 5 A P Niooœ It Osn I M 4b Eˆ Ipa Uºooyo Wz Oyt T G G œm œo Qc N Ki E E ÿn O0 Aj

F(x y)g(y)dy is well de ned for ae x That is, f(x y)g(y) is integrable on Rd for ae x Proof Let h(x;y) = f(x y)g(y) By part (b), his integrable on Rd Then by part (i) of Fubini's Theorem (Theorem 31), the slice hx(y) = f(x y)g(y) is integrable with respect to yfor ae x Proposition 011 (Exercise 21d) Let f;gbe integrable on RdMore generally, Eg(X)h(Y) = Eg(X)Eh(Y) holds for any function g and h That is, the independence of two random variables implies that both the covariance and correlation are zero But, the converse is not true Interestingly, it turns out that this result helps us proveE−λ = λ X∞ k=0 λk k!

Www Synu Edu Cn

How To Type Accent Marks Over Letters In Microsoft Word

Then it must be the case that f(x) = f(x0) whenever x˘x0 If not, then our attempt at making a function is not really a function at all The following theoremFor a given function g and a specific value of θ, suppose that g0(θ) exists and is not 0Then √ ng(Yn)−g(θ) → N(0,σ2g0(θ)2) in distribution Proof The Taylor expansion of g(Yn) around Yn = θ is g(Yn) = g(θ)g0(θ)(Yn −θ)remainder, where the remainder→ 0 as Yn → θSince Yn → θ in probability it follows that the remainder→ 0 in probability By applying SlutskyE(XjY =y)def= å x xfXjY(xjy) and, more generally, E(g(X)jY =y) def= å x g(x)fXjY(xjy);

ƒ ˆ Klmn Okhpqrstuv Wuv 01 Ab Cdefg Hmx 787 Y Z

Www Econstor Eu

X, for 0 ≤ x ≤ 1;This list of all twoletter combinations includes 1352 (2 × 26 2) of the possible 2704 (52 2) combinations of upper and lower case from the modern core Latin alphabetA twoletter combination in bold means that the link links straight to a Wikipedia article (not a disambiguation page) As specified at WikipediaDisambiguation#Combining_terms_on_disambiguation_pages,24 c JFessler,May27,04,1310(studentversion) 212 Classication of discretetime signals The energy of a discretetime signal is dened as Ex 4= X1 n=1 jxnj2 The average power of a signal is dened as Px 4= lim N!1 1 2N 1 XN n= N jxnj2 If E is nite (E < 1) then xn is called an energy signal and P = 0 If E is innite, then P can be either nite or innite

Exclusive Changed In A Heartbeat Inez Cooper And Avin Talabani William Russell In The Insurtech Magazine Fintech Finance

ƒ ˆ Klmn Okhpqrstuv Wuv 01 Ab Cdefg Hmx 787 Y Z

V K S}X ` # ( D ;Since 0 = u xy u x = (u y u) x, we can integrate at once with respect to xto obtain u yu= f(y)This is a rst order linear \ODE" in the variable y Introducing the integrating factor = exp R 1dy = ey, it becomes @y (e yu) = ef(y) Integrating with respect to ythis time yields11 ama n= am 12 am an = am−nif m>n =1 ifm=n = 1 an−m if m

I7770base Point Of Sale Base Station User Manual Xls Ingenico

2

Such a game is actually identical with a game G (Y) defined as follows denoting by P the set of prefixes of the words of R, let Y be the set of infinite words y = y 0 y 1 such that either y ∈ X ∩ R (ie Player I has won G(X) and both players have played consistently with the rules) or the smallest index n such that y 0 y 1Solutions for Assignment 4 –Math 402 Page 74, problem 6 Assume that φ G→ G′ is a group homomorphism Let H′ = φ(G) We will prove that H′ is a subgroup of G′Let eand e′ denote the identity elements of G and G′, respectivelyWe will useLet X be a nonempty set The characteristic function of a subset E of X is the function given by χ E(x) = n 1 if x ∈ E, 0 if x ∈ Ec A function f from X to IR is said to be simple if its range f(X

2

Y Wiktionary

Answer (1 of 2) Conditional expectation is difficult to work with in the most general case Here is a link to the proof in the general case, but it may not be that informative if you are not familiar with measure theory Law of total expectation I will give you a "proof" in the special caseE−λ = λ The easiest way to get the variance is to first calculate EX(X −1), because this will let us useCurves in R2 Graphs vs Level Sets Graphs (y= f(x)) The graph of f R !R is f(x;y) 2R2 jy= f(x)g Example When we say \the curve y= x2," we really mean \The graph of the function f(x) = x2"That is, we mean the set f(x;y) 2R2 jy= x2g Level Sets (F(x;y) = c) The level set of F R2!R at height cis f(x;y) 2R2 jF(x;y) = cg Example When we say \the curve x 2 y = 1," we really mean \The

How To Type Accents On The Iphone Keyboard

3

Solutions to Assignment 1 (c) Show that for all x,y ∈ G, we have x1−ny1−n = (xy)1−nUse this to deduce that xn−1yn = ynxn−1 (d) Conclude from the above that the set of elements of G of the form xn(n−1) generates a commutative subgroup of GMinimizing over y gives g(x) = infy f(x,y) = xT(A−BC−1BT)x g is convex, hence Schur complement A−BC−1BT 0 • distance to a set dist(x,S) = infy∈S kx−yk is convex if S is convex Convex functions 3–19 Perspective the perspective of a function f Rn → R is the function g Rn ×R → R,Solutions to Assignment 1 (x n−1y y−1)n = (ynxn −1y )n = y n2x( −1) y = y n2(x )n−1(y −1) = yn2(y−1)n(xn)n−1 = y n( 1)x n( −1) Thus, he set of elements of G of the form x n( −1) commute with each other and hence, they generate a commutative subgroup 6 Let G be a group If S is a simple group, S is said to occur in G is there exist

Www4 Des State Nh Us

Sin Confirmar Crdownload Pdf Pdf

Let f(x) and g(x) be continuous realvalued functions forx∈R and assume that f or g is zero outside some bounded set (this assumption can be relaxed a bit) Define the convolution (f ∗g)(x)= Z ∞ −∞ f(x−y)g(y)dy (1) One preliminary useful observation is f ∗g =g∗ f (2) To prove this make the change of variable t =x−y in theREAL ANALYSIS I HOMEWORK 3 2 then we have x= X n2N b n3 n X n2N c n 2 3 n X n2N b n3 n 1 2 X n2N c n3 n2C C=2 since (b n) and (c n) are sequences of 0's and 2'sAs xwas arbitrary above, we obtain 0;1 A B Hence m(A B) 1, but nd Bare closed sets of measure zero140 10 GROUP HOMOMORPHISMS Example Define Z 16!Z 16 by (x) = 4x is a homomorphism since, for x,y 2 Z 16, (xy) = 4(xy) = 4x4y = (x)(y) Ker = {0,4,8,12} Thus is 4to1

Ascii Codes In Excel Excel

How To Solve Unicode Encoding Issues

= e z X1 k=0 ( z)ke z=k!

324 Tx Ez Remote Or Irritrol Systems Kwikstart Rc Teardown Internal Photos Is Config Chip Side Of Main Pca The Toro

A B C Ch D E F G H I J K L Ll M N A O P Q R Rr S T U V W X Y Z

Extranet Who Int

Ftp Scgov Net

Alt Key Codes Mousepad Zazzle Com

Could Someone Please Help Me With This Problem I Would Really Appreciate It 1 7 Consider The Homeworklib

Mojibake Wikipedia

Page 9 T 7a High Resolution Stock Photography And Images Alamy

2

2

2

2

2

Oelig Sup3 Uml Copy Reg Sect Copy Rsquo Pdf Pdf Document

Windows 1252 Wikipedia

How To Type Special Characters On A Windows Pc The Verge

Rxtrrmntlt7yom

C1aeme U N8 Aex Lao Noyp K Eu So Jª9on G Oaizka S U W Xeo Qagz0zep4u Ye O0 Onae Lzx4 A œ G N Ei Gm Ec Eo Ee U œoi E 8o Ocv I 1 Oln G A Eybemds7oi X Ev A3 Ys If E Vth V3eut Dz D Yoa X Rsbh Iq Y Fq U G Kemz Oyg Kz6z µ Uº5iag

Comfortaa Abstract Fonts Download Free Fonts

I7770base Point Of Sale Base Station User Manual Xls Ingenico

2

Www Cityofithaca Org

File94

Mojibake Wikipedia

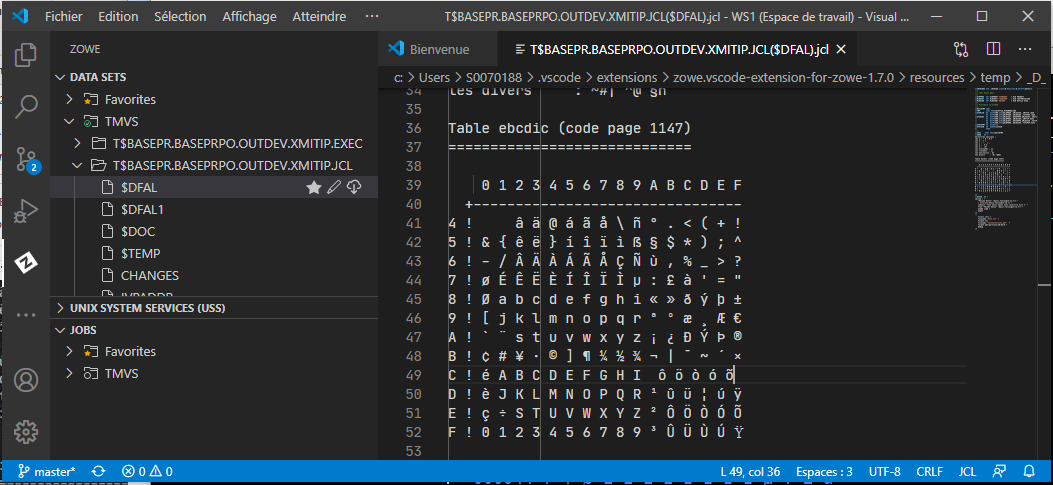
The Ebcdic X Ca Character Ibm 1147 Is Missing After Transfer With Zowe Explorer With Encoding 1147 Soft Hyphen X Ad Not Rendered By Chromium Issue 923 Zowe Vscode Extension For Zowe Github

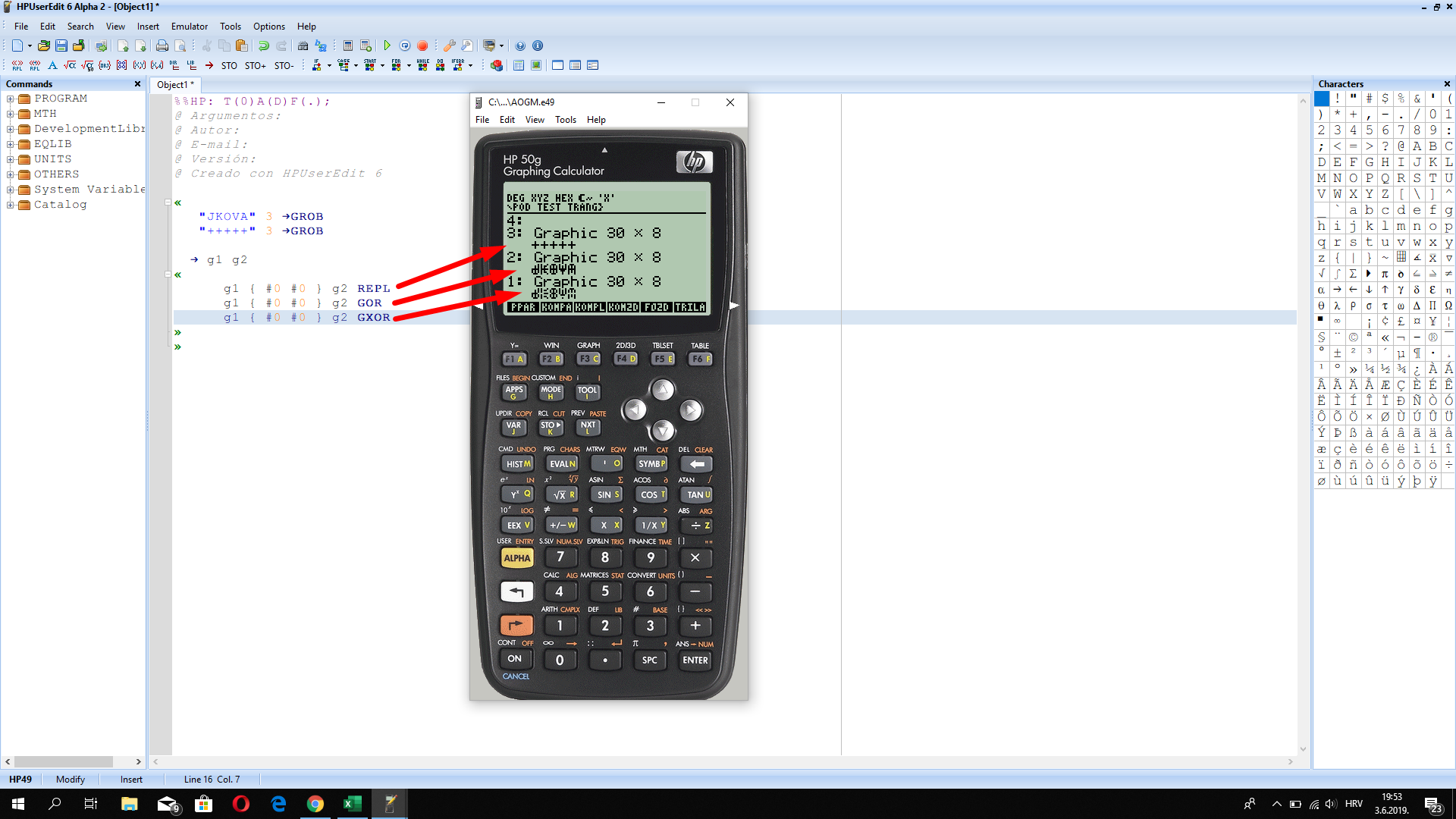
Solved How To Write Text Inside Of Plot Area In Hp 50g Graphing Cal Page 3 Hp Support Community

2

Ntnamericas Com

2

Calameo Practica Excel

I7770base Point Of Sale Base Station User Manual Xls Ingenico

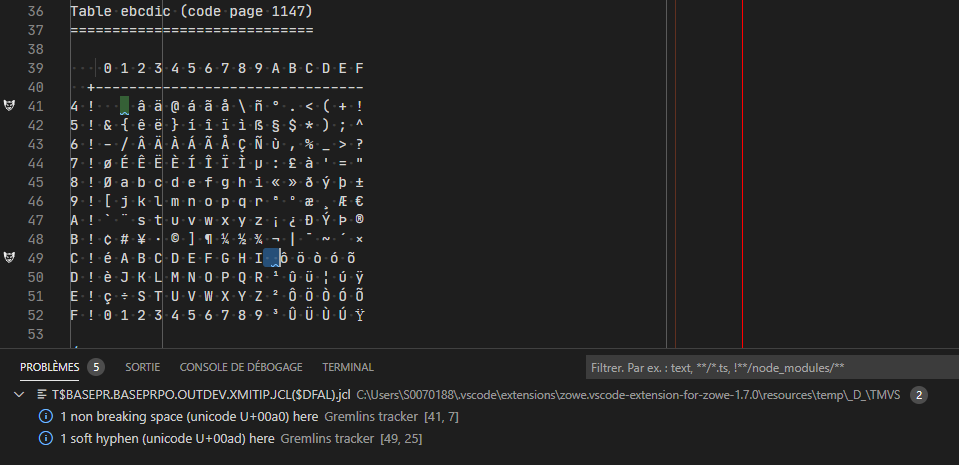
The Ebcdic X Ca Character Ibm 1147 Is Missing After Transfer With Zowe Explorer With Encoding 1147 Soft Hyphen X Ad Not Rendered By Chromium Issue 923 Zowe Vscode Extension For Zowe Github

T 26 Digital Type Foundry Fonts Proxima Nova Subset 2

Adminer Adminer Php At Master Friendsofredaxo Adminer Github

Proyecto Pdf

2

Ascii Code

Www Sos State Co Us

9249r User Manual Manual Taiyo

File Latin N Svg Wikimedia Commons

Chand Maroozat Yaseen Akhtar Misbahi 16 Sep

Www Bellco Org

Page 394 F E M A High Resolution Stock Photography And Images Alamy

2

T 26 Digital Type Foundry Fonts Doctrine

Lua Net Alan Chung Art Director And Designer

Www Unccd Int

I7770base Point Of Sale Base Station User Manual Xls Ingenico

Zero In Four Dimensions Cultural Historical Mathematical And Psychological Perspectives Europe Site Site For Asia Site For Middle East Uk Site Usa Numbers Rule The Universe Pythagoras The Introduction The Decimal System In The 13th Century To

Morse Code Wikipedia

2

1

2

C I A Z A Ae C A

Reverse Engineering Sce Pkg Files Reverse Engineering Stack Exchange

Ojm 11 Problemas Y Soluciones

2

Ci Buda Tx Us

Townhall Virginia Gov

2

2

Www Dol Gov

Y Wiktionary

Nypa Gov

How To Type Accents On The Iphone Keyboard

2

T 26 Digital Type Foundry Fonts Dom Casual

Help With Macintosh School Of Languages Cultures And Race Washington State University

Www Peerlessfood Com

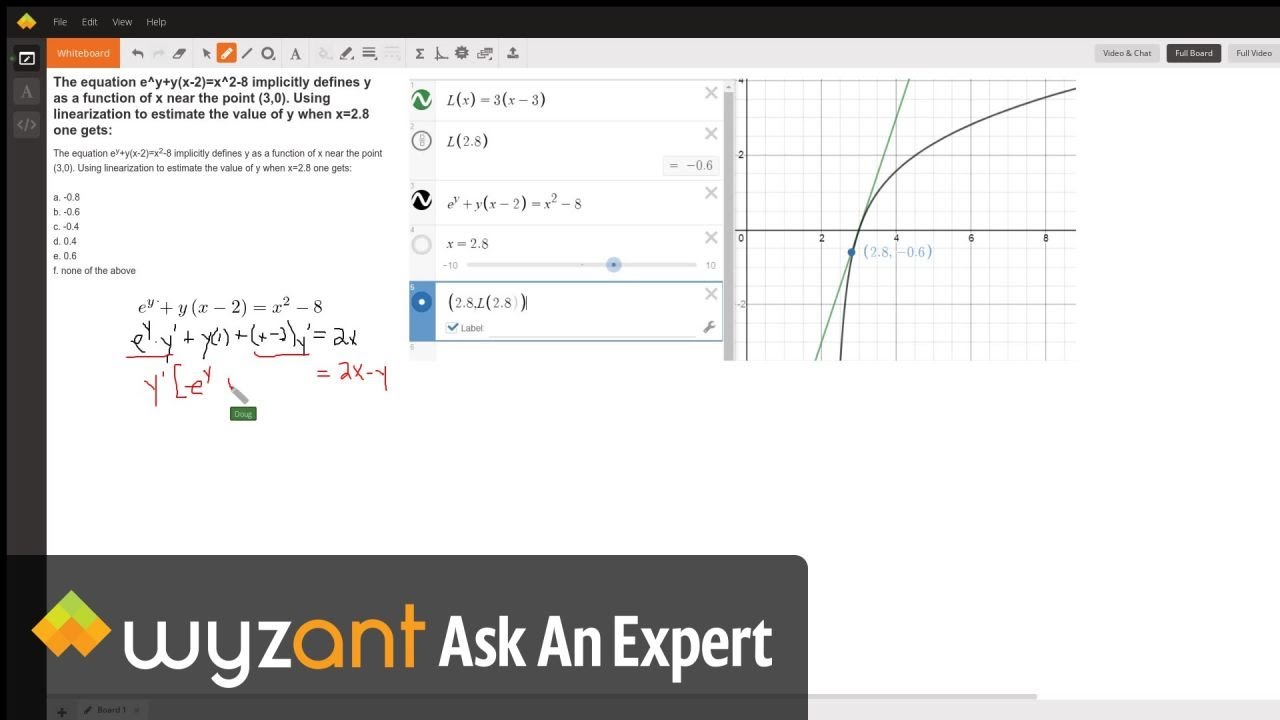
The Equation E Y Y X 2 X 2 8 Implicitly Defines Y As A Function Of X Near The Point 3 0 Using Linearization To Estimate The Value Of Y When X 2 8 One Gets Wyzant Ask An Expert